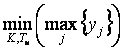5.6. Автоматическая настройка и адаптация
Естественным направлением развития коммерческих ПИД-регуляторов является разработка методов, позволяющих снизить затраты человеческого труда на их инсталляцию, настройку и обслуживание. Несмотря на то, что многие методы автоматической настройки и адаптации ПИД-регуляторов, используемые в настоящее время, были разработаны еще в 60-х годах [Справочник], в промышленных контроллерах адаптивная техника начала использоваться только с середины 80-х. Это связано с технической сложностью реализации адаптивных алгоритмов на элементной базе, которая существовала до появления микроконтроллеров.
Настройка может выполняться вручную или автоматически, без участия человека (автонастройка).
Автонастройка может выполняться полностью автоматически и "по требованию", когда человек является инициатором настройки. Полностью автоматическая настройка может инициироваться при наступлении заранее заданного условия, например, при изменении нагрузки, при изменении внешних воздействий, при изменении погрешности регулирования, или непрерывно во времени. Автоматическая настройка, инициируемая без участия человека, называется адаптацией. Примером адаптации может быть автонастройка при изменении числа яиц в инкубаторе или нагрузки на валу двигателя. Иногда термин "адаптация" трактуют более широко, как приспособление регулятора к реальному объекту на стадии ввода системы в эксплуатацию [Справочник].
Разновидностью адаптации является разомкнутое управление параметрами регулятора (табличная автонастройка), когда заранее найденные параметры регулятора для разных условий работы системы заносятся в таблицу, из которой они извлекаются при наступлении условий, по которым инициируется адаптация.
Адаптация в принципе является медленным процессом, поэтому ее нельзя рассматривать как непрерывное слежение параметров регулятора за изменяющимися параметрами объекта.
Отметим, что регуляторы, настроенные в автоматическом режиме, чаще настроены хуже, чем настроенные в ручном режиме [O'Dwyer]. Объясняется это философским рассуждением, что компьютер не может выполнять сложные и плохо формализуемые задачи лучше человека.
В настоящий момент отсутствуют простые, надежные и общепринятые методы автоматической настройки.
5.6.1. Основные принципы
Все виды автоматической настройки используют три принципиально важных этапа: идентификация, расчет параметров регулятора, настройка [Изерман]. Часто конечный этап включает этап подстройки (заключительная оптимизации настройки). Оптимизация настройки необходима в связи с тем, что методы расчета параметров регулятора по формулам являются упрощенными, не учитывают нелинейности объекта, в частности, всегда присутствующую нелинейность типа "ограничение", а идентификация параметров объекта выполняется с некоторой погрешностью. Подстройка регулятора может быть поисковой (без идентификации объекта, путем поиска оптимальных параметров) и беспоисковой (с идентификацией). Поисковая идентификация базируется обычно на правилах (см. раздел "Ручная настройка, основанная на правилах") или на итерационных алгоритмах поиска минимума критериальной функции. Наиболее распространен поиск оптимальных параметров с помощью градиентного метода поиска. Для этого находят производные от критериальной функции по параметрам ПИД-регулятора, которые являются компонентами вектора градиента. Далее производится изменение параметров в соответствии с направлением градиента.
Важно подчеркнуть, что несмотря на наличие "автоматической" подстройки, контроллер может не дать требуемого качества регулирования по причинам, не зависящим от качества заложенных в него алгоритмов. Например, объект управления может быть плохо спроектирован (зависимые контуры регулирования, большая задержка, высокий порядок объекта); объект может быть нелинейным; датчики могут быть расположены не в том месте, где нужно и иметь плохой контакт с объектом, уровень помех в канале измерения может быть недопустимо большим; разрешающая способность датчика может быть недостаточно высокой; источник входного воздействия на объект может иметь слишком большую инерционность или гистерезис; могут быть также ошибки в монтаже системы, плохое заземление, обрывы проводников и т. д. Поэтому прежде чем начинать автоматическую настройку, необходимо убедиться в отсутствии перечисленных проблем. Например, если вследствие износа механической системы появился непредусмотренный проектом гистерезис и поэтому система находится в режиме колебаний, подстройка регулятора может не дать желаемого результата, пока не устранена причина проблемы.
|
|
|
|
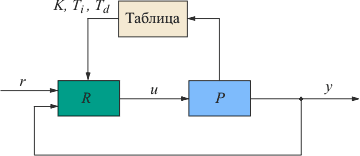
Рис. 5.87. Адаптивное управление с помощью параметров, заранее записанных в таблицу
|
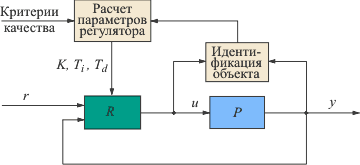
Рис. 5.88. Общая структура системы с автоматической настройкой
|
Структурная схема самонастраивающейся системы приведена на рис. 5.88. Автонастройка практически не имеет никаких особенностей по сравнению с описанными ранее методами, за исключением того, что она выполняется в автоматическом режиме. Основным этапом автоматической настройки и адаптации является идентификация модели объекта. Она выполняется в автоматическом режиме обычными методами, рассмотренными в разделе "Идентификация моделей динамических систем". Автоматическая настройка может выполняться и без идентификации объекта, основываясь на правилах (см. раздел "Ручная настройка, основанная на правилах") или поисковых методах.
5.6.2. Табличное управление
Наиболее простым методом адаптации ПИД-регулятора к изменяющимся свойствам объекта управления является табличное управление коэффициентами регулятора. Оно может быть использован не только для адаптивного управления, но и для управления нелинейными объектами, нестационарными процессами, при необходимости изменять параметры в зависимости от некоторых условий.
Принцип табличного управления очень прост (рис. 5.87). Зная заранее возможные изменения режима работы системы (например, возможные варианты загрузки инкубатора яйцами), выполняют идентификацию объекта для нескольких разных режимов и для каждого из них находят параметры регулятора. Значения этих параметров записывают в таблицу. В процессе функционирования системы измеряют величину, которая характеризует режим работы системы (например, вес яиц - с помощью датчика веса, или уровень жидкости в автоклаве с помощью датчика уровня) и в зависимости от ее значений выбирают из таблицы величины коэффициентов ПИД-регулятора.
Описанную систему можно рассматривать как систему с двумя контурами регулирования. Однако контур, служащий для адаптации, в нашем примере с уровнем жидкости в автоклаве или весом яиц в инкубаторе является разомкнутым. По этой причине табличное управление характеризуется высоким быстродействием, отсутствием ложного срабатывания или расхождения алгоритмов адаптации.
В общем случае таблица может быть многомерной; для снижения необходимой размерности таблицы можно использовать интерполяцию данных с помощью сплайна.
Недостатком этого метода являются большие затраты на предварительную идентификацию, необходимую для составления таблицы. Однако эту проблему частично можно решить применением специальных программных средств для автоматической идентификации и адаптации регулятора, после выполнения которых полученные параметры заносятся в таблицу.
Табличное управление коэффициентами регулятора целесообразно использовать в тех случаях, когда заранее известны виды и величины дестабилизируюших факторов, которые к тому же можно измерить.
5.6.3. Обзор коммерческих продуктов
Описание коммерческих продуктов, приведенное ниже, может показаться слишком неполным, непонятным и оставляет без ответа многие вопросы. Это связано с ограниченным количеством информации, которую предоставляют перечисленные ниже фирмы о своей продукции.
В подавляющем большинстве ПИД-регуляторов, защищенных патентами [Li], используются методы настройки, основанные на формулах, а не на правилах. Еще меньше контроллеров, применяющих нейронные сети и методы оптимизации. Однако доля патентов на контроллеры, использующие правила, в последние годы заметно увеличилась, в основном за счет регуляторов с нечеткой логикой (см. раздел "Нечеткая логика в ПИД-регуляторах"). Увеличилась также доля патентов на регуляторы с оптимизацией; все они используют градиентные методы, метод наименьших квадратов, эволюционные алгоритмы (см. раздел "Генетические алгоритмы").
Foxboro EXACTTM (760/761)
Foxboro была одной из первых компаний, представивших на рынок адаптивные ПИД-регуляторы. Первый адаптивный регулятор Foxboro EXACTTM (760/761), выпущенный в октябре 1984 г., был основан на распознавании образов; в дальнейшем было сделано множество модификаций в алгоритмах его функционирования. Эти алгоритмы легли также в основу построения распределенной системы управления Foxboro I/ATM. Контроллер EXACT MV> TM включает три функциональных блока: PIDA, FBTUNE и FFTUNE. PIDA является современным ПИД-контроллером, FBTUNE служит для настройки петлевого усиления, предварительной настройки и адаптации, FFTUNE выполняет настройку прямой связи в регуляторе (см. раздел "Принцип разомкнутого управления") и табличное управление.
Интегральный член регулятора выполнен в соответствии со структурой, показанной на рис. 5.58. Контроллер имеет последовательную структуру (5.84). В контроллере использована также структура, показанная на рис. 5.64 и специальная структура 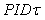 , которая является модификацией предиктора Смита. , которая является модификацией предиктора Смита.
Адаптация в контроллере основана на распознавании образов и аналогична процедуре, которую бы выполнял опытный пользователь. Применены также эвристические правила настройки (см. раздел "Ручная настройка, основанная на правилах"). Качество настройки контролируется по двум параметрам: перерегулирование и коэффициент затухания.
Контроллер имеет следующий набор параметров:
- начальные значения параметров
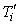 , , 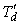 ; ;
- допустимый уровень шума
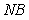 . При превышении этого уровня в 2 раза начинается процесс адаптации (автоматической настройки); . При превышении этого уровня в 2 раза начинается процесс адаптации (автоматической настройки);
- максимальное время ожидания
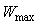 . Контроллер ждет появления второго выброса в течение времени . Контроллер ждет появления второго выброса в течение времени 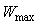 , чтобы определить период колебаний в системе. , чтобы определить период колебаний в системе.
Если пользователь не может задать перечисленные параметры, то запускается программа предварительной настройки, которая приближенно может определить эти параметры в ручном режиме (с участием пользователя). Для этого контроллер вырабатывает ступенчатый сигнал, который подается на вход объекта управления. По реакции на него определяются параметры модели первого порядка и параметры контроллера, которые вычисляются по методу Зиглера-Никольса (см. раздел "Выбор параметров регулятора"). После нахождения величины задержки 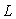 максимальное время ожидания вычисляется по формуле максимальное время ожидания вычисляется по формуле 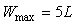 . .
Для оценки уровня шума 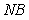 на вход объекта подают постоянный уровень сигнала и находят уровень шума на выходе, используя фильтр, чтобы исключить влияние низкочастотных внешних воздействий на результат измерений. Величину на вход объекта подают постоянный уровень сигнала и находят уровень шума на выходе, используя фильтр, чтобы исключить влияние низкочастотных внешних воздействий на результат измерений. Величину 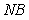 определяют как размах (от минимума до максимума) выходной переменной на осциллограмме шума. определяют как размах (от минимума до максимума) выходной переменной на осциллограмме шума.
Контроллер имеет также несколько опциональных параметров, которые принимают значения "по умолчанию", если они не заданы пользователям. К ним относятся (в скобках указаны значения "по умолчанию"):
- максимально допустимый коэффициент затухания (3,3);
- максимально допустимое перерегулирование (0,5);
- множитель при дифференциальной составляющей (1);
- диапазон подстройки (10). Этот коэффициент ограничивает диапазон автоматического изменения параметров при их подстройке. Например, если задана интегральная составляющая 10 мин., то при подстройке она не может выйти за нижнюю границу 1 мин. и верхнюю границу 100 мин.
В последних моделях регуляторов Foxboro используется двойной прямоугольный импульс (рис. 5.12-в) вместо ступенчатого воздействия в ранних версиях. Наряду с моделью первого порядка с задержкой используется модель второго порядка с задержкой. Подстройка петлевого усиления выполняется по-прежнему методом распознавания образов. Используется также метод компенсации возмущений с помощью регулятора с прямой связью (см. раздел "Принцип разомкнутого управления").
ПИД-контроллеры фирмы ABB
В контроллерах ABB адаптация основана на частотной релейной идентификации (см. раздел "Частотная идентификация в режиме релейного регулирования"). Первый адаптивный контроллер назывался ECA-40TM. Эта система также использовала метод табличного управления параметрами регулятора. Впоследствии методы адаптации дополнились непрерывной (во времени) адаптацией, адаптацией не только петлевого усиления, но и параметров прямой связи, а также методами диагностики. Перечисленные методы были воплощены в модели ECA600 TM, выпущенной в 1988 году. Эти же принципы использованы в распределенной системе управления Industrial IT System 800xA TM, которая использует еще и методы нечеткой логики и предиктивный ПИ (ППИ) регулятор.
Для идентификации используется режим релейного регулирования (см. раздел "Частотная идентификация в режиме релейного регулирования"). Для этого сначала устанавливается желаемое рабочее значение входной переменной для объекта, затем оператор нажимает кнопку автонастройки. Регулятор сначала измеряет уровень шума, затем в контур регулирования включается реле с гистерезисом, при этом алгоритм ПИД-регулирования временно отключается. Величина гистерезиса устанавливается автоматически, на основе измеренного уровня шума на выходе объекта. Чем меньше измеренный уровень шума, тем меньше может быть амплитуда колебаний в системе в режиме релейного регулирования. Амплитуда колебаний автоматически настраивается такой величины, чтобы быть выше уровня шума. После получения колебаний с установившейся амплитудой и частотой эксперимент прерывается и по его результатам вычисляется частота колебаний и коэффициент передачи объекта на этой частоте методом гармонической линеаризации (см. раздел "Частотная идентификация в режиме релейного регулирования").
Частотная идентификации в режиме релейного регулирования выполняется с применением реле с регулируемым гистерезисом (см. раздел "Частотная идентификация в режиме релейного регулирования"), что позволяет задавать частоту колебаний ниже частоты 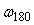 . По умолчанию колебания задаются такими, чтобы петлевое усиление контура на частоте колебаний . По умолчанию колебания задаются такими, чтобы петлевое усиление контура на частоте колебаний 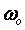 было равно было равно 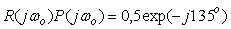 . Поскольку частотная идентификация дает только два параметра (частоту и коэффициент передачи), а ПИД-регулятор имеет три параметра, то используется дополнительное соотношение . Поскольку частотная идентификация дает только два параметра (частоту и коэффициент передачи), а ПИД-регулятор имеет три параметра, то используется дополнительное соотношение 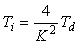 . .
Описанная процедура идентификации иногда дает очень большое усиление для объектов с малой задержкой. В этом случае используется ПИ-регулятор с коэффициентами, которые рассчитываются по формулам 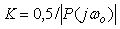 , , 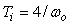 . Для объектов с большой задержкой используются формулы . Для объектов с большой задержкой используются формулы 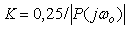 , , 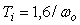 . .
Для идентификации параметров в режиме релейного регулирования используются два узкополосных фильтра, настроенных на частоту колебаний в системе 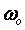 . Один из них фильтрует сигнал на входе объекта, второй - на его выходе. Фильтры позволяют получить первую гармонику ряда Фурье, которая используется в методе гармонического баланса (см. раздел "Частотная идентификация в режиме релейного регулирования"). Эта частота предварительно находится также из эксперимента с колебаниями в релейном регуляторе, методом наименьших квадратов. . Один из них фильтрует сигнал на входе объекта, второй - на его выходе. Фильтры позволяют получить первую гармонику ряда Фурье, которая используется в методе гармонического баланса (см. раздел "Частотная идентификация в режиме релейного регулирования"). Эта частота предварительно находится также из эксперимента с колебаниями в релейном регуляторе, методом наименьших квадратов.
В последних версиях контроллеров ABB после идентификации в режиме релейного регулирования используется дополнительный этап идентификации по реакции объекта на входной скачок для идентификации статического коэффициента передачи.
В контроллерах ABB используется также табличное управление (см. выше), которое используется практически во всех промышленных контроллерах и других производителей. Переменные, от которых зависят коэффициенты регулятора, выбираются пользователем. Ими могут быть управляющее воздействие на объект, выходная переменная системы или внешний сигнал. В последних версиях регуляторов были существенно расширены размеры таблиц для табличного управления. Данные для ввода в таблицу находятся путем выполнения процедуры автонастройки для нужных режимов работы объекта.
Во всех контроллерах ABB, начиная с ECA400TM, используется адаптивная прямая связь от возмущений (компенсация возмущений), которая позволяет существенно улучшить качество системы регулирования.
ПИД-контроллеры Emerson
Методы адаптивного регулирования, заложенные еще в распределенной системе управления Provox TM и RS3 TM, впоследствии были перенесены и расширены в системе DeltaV TM. Система использует автонастройку, табличное управление и адаптацию. Имеется также программное обеспечение для нечеткого регулирования и систем с транспортной задержкой.
Автоматическая настройка базируется на методе релейной идентификации. Используются несколько периодов колебаний в системе. Амплитуда колебаний выбирается равной нескольким процентам от полного динамического диапазона системы. Для оценки величины транспортной задержки используется реакция на скачок. Полученные таким способом три параметра достаточны для идентификации модели первого порядка с задержкой. Для этого используются, по выбору пользователя, метод Зиглера-Никольса, регулятор с внутренней моделью (см. раздел "Регулятор с внутренней моделью") или ламбда-тьюнинг [Astrom]. Система построена таким образом, что неопытные пользователи имеют мало опций для выбора, а опытные - много. Система имеет также встроенную подсистему моделирования, которая позволяет увидеть графики процесса регулирования до того, как коэффициенты регулятора будут записаны в контроллер.
Адаптивное управление базируется на данных, полученных из процесса во время его нормальной работы, без тестовых воздействий, а также, по выбору пользователя, с тестовыми воздействиями.
ПИД-контроллеры фирмы Honeywell
Адаптация в контроллере UDC6000TM выполняется как с помощью предварительной идентификации модели, так и на основе правил. Идентификация выполняется по отклику на скачок. Величину приращения уставки относительно рабочей точки задает пользователь. Эксперимент выполняется в разомкнутом контуре. Величина задержки определяется как время от начала эксперимента до момента, когда выходная переменная достигнет некоторого малого, наперед заданного значения.
В процессе эксперимента отслеживается величина производной от выходной переменной. Если производная все время уменьшается, выбирается модель первого порядка, параметры которой идентифицируются по нескольким точкам переходной характеристики. Идентификация выполняется на интервале, равном 1/3 от постоянной времени и заканчивается до того, как процесс в системе установится. Если производная имеет максимум, выбирается модель второго порядка и идентификация выполняется на интервале времени, включающем установившееся состояние объекта.
Контроллер UDC6000TM может работать и в режиме непрерывной адаптации, которая выполняется, как только выходная переменная изменится более чем на 0,3% (эта величина может быт изменена пользователем) от заданного значения.
5.6.4. Программные средства настройки
Типовая система для настройки ПИД-регулятора состоит из компьютера с программным обеспечением под Windows, комплекта модулей ввода-вывода и соединительных кабелей. Объект включается в контур регулирования, система настраивается желаемым способом, затем полученный коэффициенты регулятора записываются в ПИД-контроллер. Благодаря удобному пользовательскому интерфейсу, большой производительности компьютера и отсутствию ограничений на алгоритмы идентификации системы, удается получить параметры регулятора, близкие к оптимальным.
В настоящее время имеется около полусотни коммерческих продуктов [Li] для настройки ПИД-регуляторов. Среди них - Protuner фирмы Techmation Inc., LabVIEW PID Control Toolset фирмы National Instruments, Intelligent Tuner (Fisher-Rosemount), Profit PID (Honeywell) и др.
Среди аналитических методов настройки в этих программах наиболее распространены ламбда-тьюнинг [Astrom] или метод регулятора с внутренней моделью (см. раздел "Регулятор с внутренней моделью"). Подавляющее большинство программ использует модель первого порядка с задержкой для описания объекта регулирования.
Связь с оборудованием выполняется с помощью ОРС сервера, DDE, COM или DCOM технологии, среди которых только ОРС сервер является средством, основанным на международном стандарте.
Развитие описываемых средств идет в направлении расширения диапазона поддерживаемых ПИД-регуляторов, применения методов искусственного интеллекта и методов диагностики, развития пользовательского интерфейса. Современные средства настройки позволяют анализировать износ клапанов, делать оценку робастности, автоматически генерировать отчет с параметрами контура регулирования, строить графики спектральной плотности мощности и функций авто- и взаимной корреляции, делать оптимизацию инверсной модели объекта управления и т. п.
Techmation Protuner
Protuner [Techmation] - это система для настройки ПИД-регуляторов фирмы Techmation Inc. Система отображает графики переходного процесса, выполняет преобразование экспериментальных характеристик из временной области в частотную и вычисляет параметры регулятора, используя несколько различных методов настройки.
Перед началом работы системы пользователю предлагается меню для ввода априорной информации об объекте регулирования:
- диапазон изменения входного и выходного сигналов объекта;
- тип процесса в объекте управления: интегрирующий или нет;
- желаемые единицы измерения;
- структура контроллера (идеальная, последовательная или параллельная);
- частота дискретизации;
- постоянная времени фильтра в измерительном канале.
Идентификация выполняется с помощью анализа реакции на входной скачок, в замкнутом или разомкнутом контуре, по выбору пользователя. Рекомендуется вариант в разомкнутом контуре. После того, как пользователь нажимает кнопку "Старт", входной и выходной сигнал отображаются на экране компьютера.
Имеется некоторые возможности предварительной обработки собранных данных. К ним относится удаление грубых ошибок измерений и выбросов, связанных с импульсными помехами, а также цифровая фильтрация. Это позволяет выполнять эксперименты в реальных условиях индустриального окружения.
После предварительной обработки данных Protuner выполняет расчет частотной характеристики объекта, которая может быть отображена в виде диаграммы Боде, Найквиста или Никольса. Отображаются также статический коэффициент передачи, постоянные времени и транспортная задержка, частота 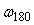 и период и период 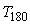 . .
Параметры ПИД-регулятора вычисляются по частотным характеристикам. Сначала вычисляются постоянная интегрирования и постоянная дифференцирования, затем, на основе заданного запаса по фазе и усилению вычисляется пропорциональный коэффициент регулятора.
Качество регулирования задается в виде понятий "сильно демпфированная" переходная характеристика, "слабо демпфированная" и "быстрая" (с коэффициентом затухания 1/0,38).
Protuner дает разные коэффициенты регулятора для реакции на изменение уставки и нагрузки.
Имеются средства для моделирования системы до записи параметров в ПИД-контроллер. Могут быть также построены частотные характеристики замкнутой системы, которые позволяют оценить полученный запас по фазе и усилению.
5.6.5 Непараметрическая модель объекта управления в ПИД-регуляторах с автоматической настройкой
Ниже предлагается алгоритм автоматической настройки и адаптации ПИД-регулятора, в основе которого лежит применение характеристик реального объекта вместо его аналитической модели [Denisenko, Денисенко], а также численных методов моделирования и оптимизации. Сама идея применения реальных приборов вместо их математических моделей разработана в книге [Денисенко] применительно к моделированию МОП-транзисторов.
Алгоритм работы большинства известных ПИД-регуляторов с автоматической настройкой или адаптацией [Astrom, Денисенко, Штейнберг, Шубладзе] состоит из следующих этапов:
- идентификация параметров модели объекта управления;
- расчет коэффициентов ПИД-регулятора;
- ввод коэффициентов в ПИД-регулятор и запуск его функционирования.
Расчет коэффициентов выполняется по формулам, которые получены аналитически. Аналитические методы используется трижды: для описания модели, для ее идентификации и для расчета параметров регулятора по уравнениям модели. Поскольку аналитические решения существуют только для простых задач, такой подход требует множества упрощающих предположений (об отсутствии нелинейности типа "ограничение", о том, что объект описывается моделью первого или второго порядка, реже моделью со специальной, но простой структурой [Шубладзе], предположение об отсутствии погрешности дискретизации, о том, что задержка является транспортной и др.[Astrom]).
Для идентификации аналитической модели в регуляторах с автоматической настройкой также используются упрощения (о пренебрежении высшими гармониками в методе гармонического баланса при идентификации по собственным колебаниям, о совпадении характеристик модели и объекта всего в нескольких точках при идентификации по реакции на скачок, о линейности модели и отсутствии эффекта "интегрального насыщения" [Astrom]).
При расчете параметров регулятора предполагается, что погрешность численного дифференцирования и интегрирования отсутствует. Предполагается также, что критерий качества регулирования задан жестко во время получения расчетных формул и в дальнейшем изменяться не может. Например, используется критерий минимума дисперсии [Ротач, экспертный критерий [Ротач], заданный декремент затухания [Ziegler], максимальная степень устойчивости [Шубладзе], и т.п. Пользователь регулятора не может задать критерий, наилучший для конкретного технологического процесса, вид переходной характеристики или робастность системы.
Вследствие принятых допущений появляется погрешность модели, по причине которой фактическая настройка регулятора не является оптимальной, даже если расчетные формулы получены из условий минимума некоторого критерия качества регулирования. Эти недостатки аналитических расчетов не видны, если при их верификации вместо эксперимента используются результаты моделирования.
В настоящей работе предлагается вместо приближенной параметрической аналитической модели использовать измеренную характеристику реального объекта управления без ее представления в аналитической форме, т.е. табличную модель переходной характеристики и интеграл Дюамеля. При этом этап параметрической идентификации исключается полностью, а расчет коэффициентов регулятора выполняется методами численного моделирования. Сочетание численных методов с точной непараметрической моделью позволяет отказаться от упрощающих допущений при расчете коэффициентов регулятора и использовать методы оптимизации. Пользователь получает возможность задавать критерий оптимальности исходя из требований конкретной задачи.
Непараметрическая модель объекта управления представляет собой свертку переходной характеристики объекта 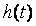 (реакции на скачок) и производной от управляющего воздействия (реакции на скачок) и производной от управляющего воздействия 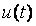 , которые заданы в дискретной форме (t=kt, k - номер отсчета, , которые заданы в дискретной форме (t=kt, k - номер отсчета, 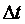 - интервал дискретизации) и поэтому не требует аналитического описания входящих в него функций. Реакция на скачок - интервал дискретизации) и поэтому не требует аналитического описания входящих в него функций. Реакция на скачок 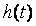 хранится в виде массива (таблицы) в памяти ПИД-контроллера. Непараметрическая модель не требует каких-либо упрощающих предположений и пригодна для линейных объектов любого порядка. Точность такой модели ограничивается только погрешностью измерений, шумами и внешними возмущениями во время измерений. хранится в виде массива (таблицы) в памяти ПИД-контроллера. Непараметрическая модель не требует каких-либо упрощающих предположений и пригодна для линейных объектов любого порядка. Точность такой модели ограничивается только погрешностью измерений, шумами и внешними возмущениями во время измерений.
Нелинейность типа "ограничение", как правило, является статическим звеном, поэтому на точность динамической части модели не влияет. Динамические нелинейности могут быть учтены аналогично, с помощью рядов Вольтерра, но этот вопрос мы рассматривать не будем.
|
|
|
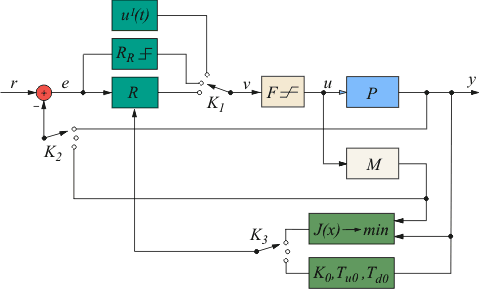
Рис. 5.87. Система управления с ПИД-регулятором
|
На основе точной непараметрической модели объекта управления в контроллере строится численная модель всей системы. С ее помощью можно предсказать поведение регулятора, и, следовательно, рассчитать его параметры 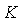 , , 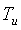 , , 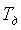 (пропорциональный коэффициент, интегральную и дифференциальную постоянные времени) методами оптимизации. (пропорциональный коэффициент, интегральную и дифференциальную постоянные времени) методами оптимизации.
Процесс адаптации регулятора с непараметрической моделью выполняется обычными методами [Astrom]. Отличие состоит только в отсутствии этапа параметрической идентификации.
Рассмотрим особенности практической реализации изложенного принципа для построения оптимального ПИД-контроллера с автоматической настройкой или адаптацией. Структурная схема системы управления с предлагаемым контроллером показана на рис. 5.87. Здесь 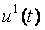 - источник ступенчатого тестового воздействия; - источник ступенчатого тестового воздействия; 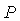 - объект управления; - объект управления; 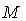 - его параметрическая модель; - его параметрическая модель; 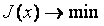 - блок оптимизации; - блок оптимизации; 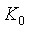 , , 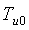 , , 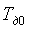 - блок поиска начального приближения коэффициентов регулятора; - блок поиска начального приближения коэффициентов регулятора; 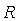 - ПИД-регулятор; - ПИД-регулятор; 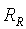 - релейный регулятор. Смысл остальных обозначений будет расшифрован по ходу изложения. - релейный регулятор. Смысл остальных обозначений будет расшифрован по ходу изложения.
Алгоритм работы регулятора в режиме автоматической настройки состоит из следующих этапов.
- Оценка начальных приближений коэффициентов
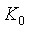 , , 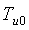 , , 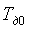 . .
- Вывод регулятора в рабочую точку.
- Измерение реакции на прямоугольный импульс.
- Сглаживание полученной характеристики.
- Моделирование ПИД-регулятора и оптимизация его коэффициентов.
- Переход на работу в обычном режиме ПИД-регулирования с оптимальными коэффициентами.
Оценка начальных приближений коэффициентов регулятора выполняется в режиме автоколебаний [Денисенко, Astrom]. Для этого на рис. 5.87 переключатель 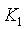 (здесь и ниже имеется в виду программное переключение) устанавливается в среднее положение, (здесь и ниже имеется в виду программное переключение) устанавливается в среднее положение, 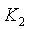 - в верхнее, - в верхнее, 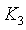 - в нижнее. Релейный регулятор - в нижнее. Релейный регулятор 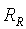 представляет собой безынерционный нелинейный элемент с характеристикой представляет собой безынерционный нелинейный элемент с характеристикой
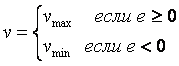 , , |
(1)
|
где 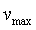 и и 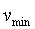 выбираются так, чтобы амплитуда колебаний в замкнутой системе не превысила технологически допустимые пределы. Отметим, что мы не согласны с мнением некоторых авторов [Штейнберг], что режим автоколебаний является опасным для технологического процесса и следует избегать его применения. Он ничуть не опаснее подачи прямоугольного или иного тестового импульса, если ограничить амплитуду автоколебаний безопасными пределами. Режим автоколебаний успешно используется в подавляющем большинстве промышленных ПИД-контроллеров, см. [Денисенко,Astrom]. выбираются так, чтобы амплитуда колебаний в замкнутой системе не превысила технологически допустимые пределы. Отметим, что мы не согласны с мнением некоторых авторов [Штейнберг], что режим автоколебаний является опасным для технологического процесса и следует избегать его применения. Он ничуть не опаснее подачи прямоугольного или иного тестового импульса, если ограничить амплитуду автоколебаний безопасными пределами. Режим автоколебаний успешно используется в подавляющем большинстве промышленных ПИД-контроллеров, см. [Денисенко,Astrom].
Ограничение амплитуды автоколебаний выполняется следующим образом. Размах переменной на выходе релейного блока 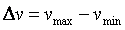 выбирают равным выбирают равным 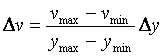 , где , где 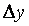 - технологически допустимый размах автоколебаний, заданный оператором; - технологически допустимый размах автоколебаний, заданный оператором; 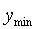 , , 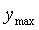 - минимальное и максимальное значение выходной переменной, соответствующее минимальному и максимальному значению управляющего воздействия - минимальное и максимальное значение выходной переменной, соответствующее минимальному и максимальному значению управляющего воздействия 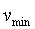 , , 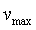 . Например, для печи . Например, для печи 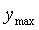 - это установившееся значение температуры при - это установившееся значение температуры при 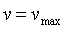 , , 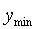 - температура при - температура при 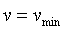 . .
Величины 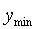 , , 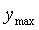 могут быть известны из эксплуатационной документации на объект управления, измерены в отдельном тесте по реакции на скачок или найдены по характерным точкам переходного процесса во время вывода системы в режим автоколебаний. могут быть известны из эксплуатационной документации на объект управления, измерены в отдельном тесте по реакции на скачок или найдены по характерным точкам переходного процесса во время вывода системы в режим автоколебаний.
Желательно, чтобы величины 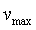 и и 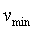 располагались симметрично относительно среднего значения располагались симметрично относительно среднего значения 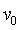 , которое можно определить из пропорции , которое можно определить из пропорции
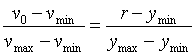 , , |
(2)
|
|
|
|
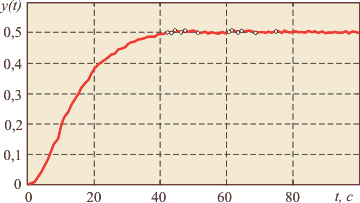
Рис. 5.88 Перевод системы в режим собственных колебаний (участок колебаний в масштабе с увеличением показан на рис. 5.89)
|
где 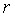 - заданное значение уставки. Симметрия - заданное значение уставки. Симметрия 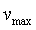 и и 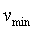 обеспечивает симметрию колебаний в системе относительно значения уставки обеспечивает симметрию колебаний в системе относительно значения уставки 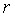 . .
Приведенные формулы являются точными для линейного объекта и их погрешность возрастает с ростом нелинейности. Однако для практики погрешность таких оценок в большинстве случаев достаточна. Кроме того, характер нелинейности у тепловых объектов таков, что фактический режим оказывается более безопасным, чем рассчитанный по приведенным формулам.
На рис. 5.88 показан экспериментально полученный график вывода системы в режим автоколебаний, для которого значения 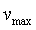 и и 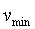 рассчитаны по формулам (1), (2). Точками обозначены отсчеты собранных данных, кружочки показывают моменты перехода рассчитаны по формулам (1), (2). Точками обозначены отсчеты собранных данных, кружочки показывают моменты перехода 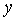 через уровень через уровень 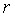 . Как видим, амплитуда колебаний достаточно мала, чтобы говорить о ее опасности для технологического процесса (см. также участок колебаний в масштабе с увеличением на рис. 5.89). . Как видим, амплитуда колебаний достаточно мала, чтобы говорить о ее опасности для технологического процесса (см. также участок колебаний в масштабе с увеличением на рис. 5.89).
Алгоритм поиска участка автоколебаний определяет три точки перехода 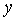 через уровень через уровень 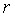 , чтобы выделить один период колебаний. Для увеличения надежности алгоритма при наличии шума используется принцип мажоритарного голосования: измеряются три точки и решение о превышении уставки принимается, если две из трех точек выше уровня , чтобы выделить один период колебаний. Для увеличения надежности алгоритма при наличии шума используется принцип мажоритарного голосования: измеряются три точки и решение о превышении уставки принимается, если две из трех точек выше уровня 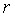 . Начальное приближение оценки периода автоколебаний становится известным уже после мажоритарного голосования. Данные в течение не менее чем одного периода сохраняются в массив для последующей идентификации амплитуды . Начальное приближение оценки периода автоколебаний становится известным уже после мажоритарного голосования. Данные в течение не менее чем одного периода сохраняются в массив для последующей идентификации амплитуды 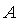 и уточнения периода и уточнения периода 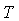 функции функции
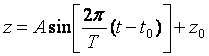 , , |
(3)
|
|
|
|
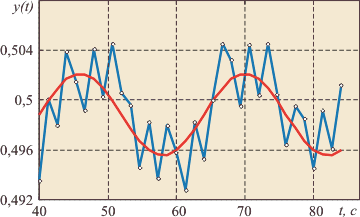
Рис. 5.89 Подгонка функции (3) (красная линия) к экспериментальным данным (синяя линия)
|
где 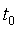 , , 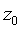 сдвиг по времени и уровню. сдвиг по времени и уровню.
Идентификация выполняется путем минимизации квадратичной нормы 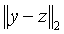 методом покоординатного спуска последовательно по координатам методом покоординатного спуска последовательно по координатам 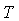 , , 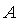 , , 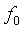 , , 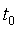 . Ряд экспериментов с тепловыми объектами показал, что критериальная функция является унимодальной овражной. Для ускорения движения к минимуму использован крупный шаг. Благодаря хорошему начальному приближению периода колебаний минимум с удовлетворительной точностью находится за 5...10 шагов по каждой координате. Полученные параметры . Ряд экспериментов с тепловыми объектами показал, что критериальная функция является унимодальной овражной. Для ускорения движения к минимуму использован крупный шаг. Благодаря хорошему начальному приближению периода колебаний минимум с удовлетворительной точностью находится за 5...10 шагов по каждой координате. Полученные параметры 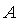 и и 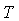 используются для расчета начальных приближений параметров используются для расчета начальных приближений параметров 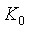 , , 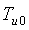 , , 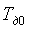 методом Зиглера-Никольса [Ziegler]. методом Зиглера-Никольса [Ziegler].
На рис. 5.89 показан выбранный из рис. 5.88 и увеличенный участок кривой для идентификации, а также результат подгонки синусоидального "шаблона" (3) к собранным данным. Амплитуда колебаний составляет всего 0,4% от значения уставки, тем не менее, описанный метод надежно выделяет сигнал на фоне шума и находит параметры 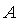 и и 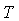 . .
После оценки начальных приближений 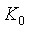 , , 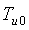 , , 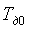 регулятор переходит в режим ПИД-регулирования (на рис. 5.88 это участок после последней точки, помеченной кружочком, а на рис. 5.87 переключатель регулятор переходит в режим ПИД-регулирования (на рис. 5.88 это участок после последней точки, помеченной кружочком, а на рис. 5.87 переключатель 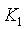 устанавливается в нижнее положение, устанавливается в нижнее положение, 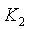 - в верхнее, - в верхнее, 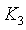 - в среднее). - в среднее).
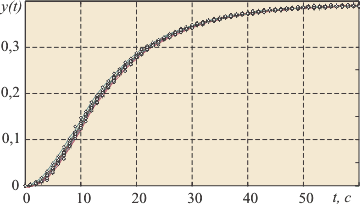
После установки стационарного уровня 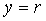 выполняется измерение реакции объекта выполняется измерение реакции объекта 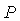 на скачок на скачок 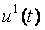 (на рис. 5.87 переключатель (на рис. 5.87 переключатель 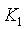 переводится в верхнее положение, переводится в верхнее положение, 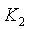 - в среднее). Величина скачка выбирается как можно большей, но не более максимально допустимой для конкретного технологического процесса. Факт стационарности устанавливается как отсутствие выхода - в среднее). Величина скачка выбирается как можно большей, но не более максимально допустимой для конкретного технологического процесса. Факт стационарности устанавливается как отсутствие выхода 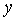 за границы допустимой погрешности в течение времени за границы допустимой погрешности в течение времени 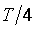 . На рис. 5.90 точками показана экспериментально полученная переходная характеристика объекта для пяти последовательно выполненных измерений, приведенная к единичному скачку на входе. Разброс точек объясняется шумом и внешними возмущениями во время измерений. Сплошными линиями на рис. 5.90 показаны результаты сглаживания экспериментальных данных сплайнами третьей степени [9]. . На рис. 5.90 точками показана экспериментально полученная переходная характеристика объекта для пяти последовательно выполненных измерений, приведенная к единичному скачку на входе. Разброс точек объясняется шумом и внешними возмущениями во время измерений. Сплошными линиями на рис. 5.90 показаны результаты сглаживания экспериментальных данных сплайнами третьей степени [9].
В процессе сглаживания сплайном минимизируется функционал [Dierckx]
 , , |
(4)
|
|
|
|
Рис. 5.90. Экспериментально измеренная реакция объекта управления на скачок (точки) и результат их сглаживания сплайном (сплошные линии). Приведены результаты для 5-ти экспериментов.
|
где 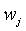 - значения весовой функции в точках - значения весовой функции в точках 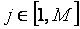 , , 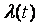 - кусочно-линейная весовая функция, определяющая степень натяжения сплайна между точками - кусочно-линейная весовая функция, определяющая степень натяжения сплайна между точками 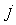 и и 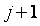 , , 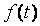 - непрерывная функция, описывающая сплайн, - непрерывная функция, описывающая сплайн, 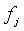 - значения функции - значения функции 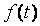 в узлах в узлах 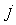 . Для получения графика, показанного на рис. 5.90, было принято . Для получения графика, показанного на рис. 5.90, было принято 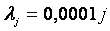 , , 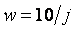 , , 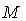 =60. =60.
После выполнения сглаживания сплайн табулируется с шагом 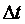 и хранится для дальнейшего использования в виде массива и хранится для дальнейшего использования в виде массива 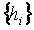 , , 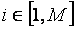 . При . При 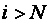 считается, что считается, что 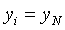 . Сглаживание сплайном 3 степени по 100 точкам занимает 0,07 с на компьютере с процессором Pentium 4, частота 2,8 ГГц. . Сглаживание сплайном 3 степени по 100 точкам занимает 0,07 с на компьютере с процессором Pentium 4, частота 2,8 ГГц.
Отметим, что шумы и внешние возмущения, не сглаженные сплайном, становятся видны при моделировании замкнутой системы. Поэтому сплайн должен иметь достаточную степень натяжения для сглаживания не только высокочастотных шумов, но и низкочастотных возмущений. Наилучшие результаты можно получить, используя сглаживающий сплайн с ограничением не только на степень натяжения, но и на его форму [Dierckx].
Вероятно, вместо сплайна можно было использовать полиномиальное сглаживание, которое требует гораздо меньше вычислительных ресурсов, но нами этот вопрос не исследован.
Следующим шагом алгоритма автонастройки является моделирование замкнутой системы с целью нахождения оптимальных коэффициентов регулятора (на рис. 5.87 переключатель 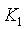 и и 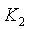 в нижнем положении, в нижнем положении, 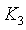 - в верхнем. Модель системы описывается системой интегро-дифференциальных уравнений - в верхнем. Модель системы описывается системой интегро-дифференциальных уравнений
где 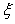 - переменная интегрирования, смысл других обозначений указан выше или ясен из рис. 5.87. - переменная интегрирования, смысл других обозначений указан выше или ясен из рис. 5.87.
Методы численного моделирования уравнения (5) описаны в работах [Astrom, Денисенко, Штейнберг, Шубладзе]. Отметим, что при моделировании системы (5)-(8) используются уже сглаженные данные, поэтому дополнительная фильтрация для вычисления производной не требуется.
В уравнении (8) использовано начальное условие 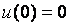 , поскольку моделирование всегда начинается после установления стационарного состояния в системе. Поэтому интеграл свертки (8) в дискретной форме вычисляется как , поскольку моделирование всегда начинается после установления стационарного состояния в системе. Поэтому интеграл свертки (8) в дискретной форме вычисляется как
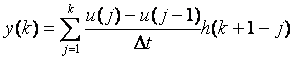 . . |
(9)
|
Для проверки адекватности полученной численной модели было выполнено сравнение режима автоколебаний в модели (черные линии на рис. 5.91) и реальной системе (серые линии). Для учета шума и внешних возмущений на рис. 5.91 приведены результаты пяти экспериментов, выполненных последовательно. Интервал между отсчетами 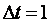 с. Разброс кривых вполне соответствует погрешности эксперимента, связанной с дискретностью отсчетов (20 отсчетов на период автоколебаний, 4 отсчета на задержку). с. Разброс кривых вполне соответствует погрешности эксперимента, связанной с дискретностью отсчетов (20 отсчетов на период автоколебаний, 4 отсчета на задержку).
На следующем шаге алгоритма автонастройки построенная численная модель системы используется для оценки оптимальных параметров регулятора. В качестве критерия оптимальности используется минимум перерегулирования:
найти 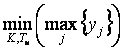 |
(10)
|
при ограничении на максимально допустимое время достижения выходной переменной 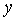 уровня уставки уровня уставки 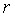 (это параметр задает пользователь) и втором ограничении, что переменная (это параметр задает пользователь) и втором ограничении, что переменная 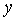 должна хотя бы один раз пересечь уровень уставки должна хотя бы один раз пересечь уровень уставки 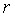 . .
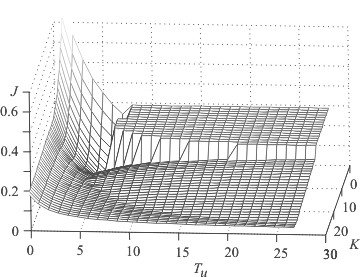
Для наглядности результатов исследования оптимизация выполнялась только по двум параметрам: 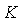 и и 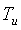 , что позволило изобразить график целевой функции в виде поверхности (рис. 5.92). Возвышенность с резкими границами отделяет участок поверхности, образованный функцией штрафа, с помощью которой учитываются ограничения. Критериальная функция является унимодальной с одним оврагом. , что позволило изобразить график целевой функции в виде поверхности (рис. 5.92). Возвышенность с резкими границами отделяет участок поверхности, образованный функцией штрафа, с помощью которой учитываются ограничения. Критериальная функция является унимодальной с одним оврагом.
Поиск минимума выполнялся методом градиентного спуска с постоянным шагом. Для устранения эффекта замедления алгоритма на дне оврага использовался крупный шаг. Процесс оптимизации, начинающийся от начального приближения, полученного методом Зиглера-Никольса (см. выше) требует около 10-30 вычислений критериальной функции и выполняется на компьютере с процессором Pentium-4 с частотой 2,8 ГГц за время менее 1 с.
Использовался также второй критерий оптимальности - минимум времени регулирования при ограничении на декремент затухания.
 |
 |
|
Рис. 5.93. Результат оптимизации по критерию минимума перерегулирования для четырех шагов спуска по направлению градиента (красная линия - результат оптимизации)
|
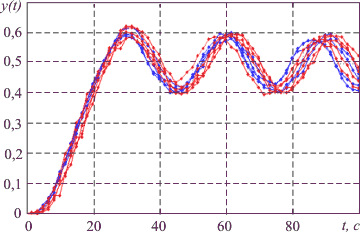
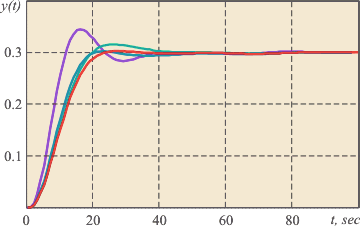
Рис. 5.94. Сравнение реакции на скачок уставки модели (красная линия) и объекта (лини других цветов)
|
Важно, что пользователь может самостоятельно задавать желаемую форму переходного процесса с помощью параметров, входящих в критерии оптимальности. После записи найденных оптимальных параметров в ПИД –регулятор он начинает работать традиционным образом.
В качестве примера на рис. 5.94 показан один из результатов оптимального (в смысле оптимального соответствия представлениям пользователя) переходного процесса (сплошная линия) и реакция реальной системы (три штриховые линии), использующей полученные результаты оптимизации.
Отметим, что в систему (5)-(8) входит нелинейный элемент 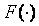 , т.е. оптимизация выполняется с учетом нелинейности и эффекта интегрального насыщения, что недостижимо в аналитических методах. , т.е. оптимизация выполняется с учетом нелинейности и эффекта интегрального насыщения, что недостижимо в аналитических методах.
Описанные выше экспериментальные результаты были получены с помощью компьютера в качестве ПИД-контроллера и модулей ввода-вывода серии RealLab! фирмы RealLab!. Объектом управления в экспериментах служил миниатюрный электропаяльник с датчиком в виде термопары без защитной оболочки. Объект управления специально выбирался с малой инерционностью, чтобы за приемлемое время на нем можно было выполнить большое число экспериментов.
Выводы
Предложенный метод построения ПИД-регулятора позволяет исключить из процесса автоматической настройки этап параметрической идентификации модели и связанные с ним погрешности, а также учесть нелинейность и интегральное насыщение. Осуществимость и эффективность метода доказана экспериментально.
Применение непараметрической модели в виде интеграла свертки в сочетании с численными методами оптимизации позволило получить оптимальные значения параметров регулятора, задавать желаемый критерий оптимальности и тем самым повысить качество регулирования.
Недостатком метода является большой объем вычислений на этапе оценки параметров (но не на этапе регулирования). Поэтому метод может быть использован в самонастраивающихся и адаптивных системах управления, построенных на основе промышленных компьютеров или мощных ПЛК, а также при управлении очень инерционными тепловыми процессами. Вероятно, его можно использовать в автономных ПИД регуляторах, построенных на базе цифровых сигнальных процессоров, имеющих аппаратную реализацию операции свертки, но нами это вопрос не исследован. В то же время, высокие темпы роста производительности универсальных микроконтроллеров позволяют надеяться на возможность реализации в будущем алгоритма в автономных ПИД-регуляторах широкого применения.
|



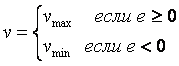 ,
,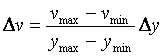 , где
, где 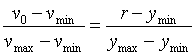 ,
,
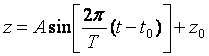 ,
,
 ,
,
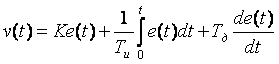 ,
,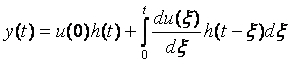 ,
,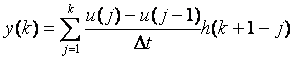 .
.