4.2. Многократные измерения
Одной из наиболее распространенных операций, выполняемых в системах сбора данных и управления, является усреднение результатов многократных измерений. Интуитивно ясно, что этот процесс приводит к повышению точности, поскольку результаты отдельных измерений имеют как положительные, так и отрицательные отклонения от точного значения и поэтому частично взаимно компенсируются. С ростом числа измерений среднее значение отрицательных отклонений приближается по модулю к среднему значению положительных отклонений и точность их взаимной компенсации улучшается. Для практики важно получить количественную зависимость между числом измерений и погрешностью усредненного результата.
4.2.1. Повышение точности путем усреднения результатов измерений
Рассмотрим некоторое средство измерений, например, измерительный модуль аналогового ввода NL-8AI для измерения и ввода в компьютер значений напряжения 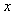 (рис. 4.4). В общем случае на датчик, линию связи между датчиком и модулем и сам модуль действуют электромагнитные помехи и собственные шумы операционных усилителей, АЦП, резисторов, микропроцессорной части модуля и т. п. [Денисенко, Денисенко]. Мы не будем рассматривать помехи, действующие на объект измерений, поскольку он не входит в состав измерительного канала. (рис. 4.4). В общем случае на датчик, линию связи между датчиком и модулем и сам модуль действуют электромагнитные помехи и собственные шумы операционных усилителей, АЦП, резисторов, микропроцессорной части модуля и т. п. [Денисенко, Денисенко]. Мы не будем рассматривать помехи, действующие на объект измерений, поскольку он не входит в состав измерительного канала.
|
|
|
Рис. 4.4. Модуль ввода измеряет физическую величину 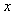 и выдает случайную величину и выдает случайную величину 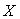
|
Указанные причины приводят к тому, что результат измерения становится случайной величиной, значение которой изменяется от измерения к измерению. Случайная величина 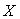 может быть описана некоторой функцией распределения c математическим ожиданием может быть описана некоторой функцией распределения c математическим ожиданием 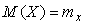 и среднеквадратическим отклонением и среднеквадратическим отклонением 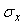 , которое принимается за случайную составляющую погрешности измерительного прибора. Дисперсия случайной величины , которое принимается за случайную составляющую погрешности измерительного прибора. Дисперсия случайной величины 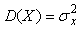 . .
Погрешность средства измерений определяется изготовителем и указывается в эксплуатационной документации. В величину погрешности входит как систематическая, так и случайная составляющая. Если случайная составляющая превышает 10% от систематической, то она указывается отдельно (ГОСТ 8.009 [ГОСТ]). В некоторых случаях случайная составляющая указывается с помощью автокорреляционной функции или спектральной плотности мощности.
Случайная составляющая погрешности может быть снижена путем усреднения результатов многократных измерений. Если в составе погрешности преобладает систематическая компонента, то усреднение не приводит к повышению точности. О наличии случайной составляющей можно судить по рассеянию результатов однократных измерений.
Предположим, что с помощью измерительного модуля выполнено 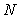 измерений, в результате которых получены значения измерений, в результате которых получены значения 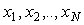 . Усреднение результатов измерений выполняется по формуле среднего арифметического . Усреднение результатов измерений выполняется по формуле среднего арифметического
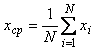 . . |
(4.39)
|
Однако 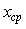 также является случайной величиной, поскольку, выполняя несколько серий измерений и усредняя каждую из их, мы получим отличающиеся друг от друга средние значения также является случайной величиной, поскольку, выполняя несколько серий измерений и усредняя каждую из их, мы получим отличающиеся друг от друга средние значения 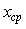 для каждой серии. Но для каждой серии. Но 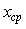 будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем измерительный прибор. Покажем это. будет иметь меньшую дисперсию (среднеквадратическое отклонение), чем измерительный прибор. Покажем это.
Будем считать, что результаты измерений 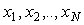 являются независимыми случайными величинами. Тогда дисперсия их среднего арифметического будет равна являются независимыми случайными величинами. Тогда дисперсия их среднего арифметического будет равна
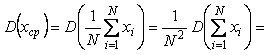  |
(4.40)
|
откуда
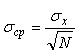 , , |
(4.41)
|
поскольку 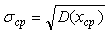 . .
В (4.40) использованы два свойства оператора дисперсии: а) дисперсия произведения случайной величины и константы равна дисперсии случайной величины, умноженной на квадрат константы и б) дисперсия суммы случайных величин равна сумме дисперсий каждой из них [Гмурман]. Кроме того, считается, что все измерения выполнены одним и тем же прибором, т.е. дисперсии всех измерений одинаковы и равны 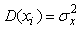 , а случайные величины являются некоррелированными. , а случайные величины являются некоррелированными.
Докажем первое из использованных свойств. По определению дисперсии 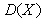 и математического ожидания и математического ожидания 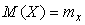 случайной величины случайной величины 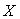
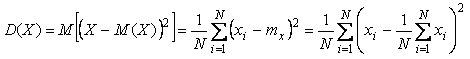 . . |
(4.42)
|
Поэтому, умножая 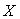 на константу на константу 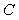 , получим: , получим: 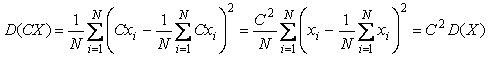 . .
Докажем теперь, что дисперсия суммы случайных величин равна сумме их дисперсий. Для этого сначала докажем, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
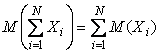 . . |
(4.43)
|
Сумма случайных величин 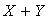 - это такая случайная величина, которая принимает все возможные комбинации сумм случайных величин - это такая случайная величина, которая принимает все возможные комбинации сумм случайных величин 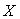 и и 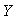 , т.е. , т.е. 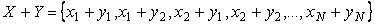 . Поэтому по определению математического ожидания . Поэтому по определению математического ожидания
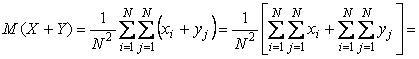 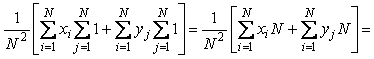 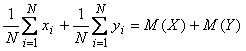 . Аналогичное соотношение для . Аналогичное соотношение для 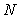 случайных величин можно доказать путем попарной группировки случайных величин. Формула (4.43) доказана. случайных величин можно доказать путем попарной группировки случайных величин. Формула (4.43) доказана.
Выведем еще вспомогательное равенство, связывающее дисперсию случайной величины с математическим ожиданием. Пользуясь определением дисперсии (4.42), получим: 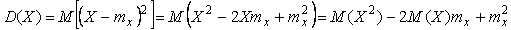 . .
Поскольку 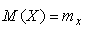 , получим , получим
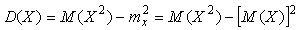 . . |
(4.44)
|
Пользуясь соотношениями (4.43) и (4.44), получим дисперсию суммы двух случайных величин в виде
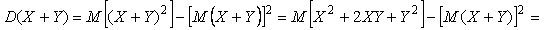 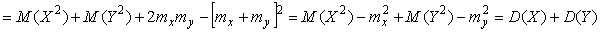 . .
Итак, усреднение 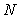 некоррелированных измерений (см. (3.2)) позволяет уменьшить погрешность результата в некоррелированных измерений (см. (3.2)) позволяет уменьшить погрешность результата в 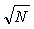 раз. Однако это утверждение справедливо при соблюдении нескольких условий, выполнимость которых довольно трудно проверить на практике. раз. Однако это утверждение справедливо при соблюдении нескольких условий, выполнимость которых довольно трудно проверить на практике.
Во-первых, усреднение дает эффект только для случайной составляющей погрешности. Погрешность измерений перестает уменьшаться, когда 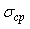 становится настолько малой, что суммарная погрешность определяется систематической составляющей. Систематическая погрешность складывается из нелинейности АЦП и операционных усилителей, температурной зависимости напряжения смещения нуля и коэффициента передачи измерительного канала (температурно-зависимые погрешности учитываются как дополнительные), низкочастотных шумов, у которых время автокорреляции больше времени выполнения серии повторных измерений (к ним относится, в частности, "старение" элементов), динамической погрешности. Практически редко удается снизить общую погрешность измерений более чем в 2...3 раза с помощью усреднения. становится настолько малой, что суммарная погрешность определяется систематической составляющей. Систематическая погрешность складывается из нелинейности АЦП и операционных усилителей, температурной зависимости напряжения смещения нуля и коэффициента передачи измерительного канала (температурно-зависимые погрешности учитываются как дополнительные), низкочастотных шумов, у которых время автокорреляции больше времени выполнения серии повторных измерений (к ним относится, в частности, "старение" элементов), динамической погрешности. Практически редко удается снизить общую погрешность измерений более чем в 2...3 раза с помощью усреднения.
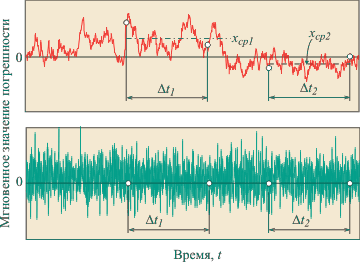
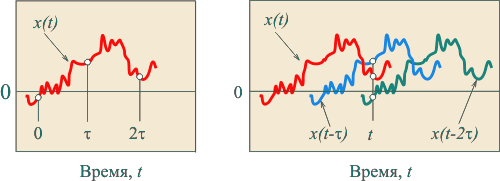
Во-вторых, результаты измерений должны быть статистически независимы, т.е. интервал времени между соседними измерениями должен быть много больше времени автокорреляции случайной погрешности. Посмотрим на рис. 4.5: если при белом шуме средние значения за интервал времени 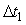 и и 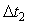 равны между собой (внизу), то при коррелированном шуме - не равны (вверху). К примеру, усреднение 100 измерений в течение 10 с не может скомпенсировать компоненты шума, спектр которых лежит ниже 0,1 Гц. равны между собой (внизу), то при коррелированном шуме - не равны (вверху). К примеру, усреднение 100 измерений в течение 10 с не может скомпенсировать компоненты шума, спектр которых лежит ниже 0,1 Гц.
В частности, требование статистической независимости измерений не выполняется также в случае, когда действует искусственная помеха, делающая шум цветным (коррелированным), например, помеха от сотового передатчика на крыше здания, от радиотелефона, из сети 50 Гц, от сварочного аппарата, от молнии, от внутренних генераторов измерительного прибора, от электродрели и т. п. В этих случаях усреднение также ослабляет помеху, но уже не в 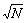 раз, подробнее см. следующий параграф. раз, подробнее см. следующий параграф.
Описанный эффект имеет место только для тех законов распределения случайной величины, для которых существует понятие среднего и среднеквадратического отклонения. Например, для распределения Коши интегралы, дающие названные определения, расходятся [Косарев].
Особо следует отметить, что как систематическая, так и случайная составляющая погрешности средств измерений являются случайными величинами. Однако между ними имеется принципиальное различие. Систематическая погрешность является случайной на множестве средств измерений, но детерминированной для каждого образца из множества. Поэтому систематическую погрешность невозможно уменьшить путем многократных измерений одним и тем же прибором, но можно уменьшить, усредняя результаты, полученные измерением с помощью множества средств измерений одного типа. Случайная же погрешность является случайной на множестве результатов измерений одним и тем средством измерений и поэтому ее можно уменьшить путем усреднения результатов многократных измерений.
В отличие от погрешности, разрешающая способность не зависит от величины систематической погрешности и поэтому может быть увеличена существенно. Она может стать даже меньше величины младшего значащего разряда АЦП при условии, если стабильность его уровней позволяет это сделать. На этом эффекте основан принцип действия дельта-сигма АЦП.
Если в паспорте на средство измерения не указана величина случайной составляющей погрешности, ее можно оценить по результатам измерений [Орнатский]:
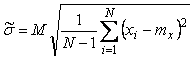 , , |
(4.45)
|
где коэффициент 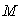 зависит от количества измерений зависит от количества измерений 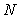 . При . При 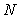 >60 он равен единице, при >60 он равен единице, при 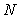 <60 о выборе этого коэффициента см. в книге [Орнатский]. <60 о выборе этого коэффициента см. в книге [Орнатский].
Вопросам повышения точности путем многократных измерений посвящен ГОСТ 8.207-76 [ГОСТ].
4.2.2. Точность и продолжительность измерений
При использовании описанной выше процедуры усреднения результатов измерений никак не учитывалось, за какое время выполняется серия измерений, поскольку предполагалось, что погрешность является некоррелированным (белым) шумом. Ниже будут рассмотрены эффекты, которые возникают в реальных условиях, когда шум измерений является цветным. Попутно станет ясно, почему точные измерительные приборы работают медленно.
Измерительные каналы средств автоматизации обычно являются частью систем, компоненты которых распределены в пространстве и соединены между собой кабельными линиями. Поэтому на них воздействует весь спектр помех, имеющихся в конкретной электромагнитной обстановке. Основными компонентами случайной погрешности, вызванной помехами, являются белый шум, фликкер (1/f) шум и относительно узкополосные помехи от работающего электрооборудования, передатчиков и естественных источников электромагнитного излучения.
Пример одной реализации белого шума (некоррелированной погрешности измерения) показан на рис. 4.5, внизу. Характерной его особенностью является то, что при изменении масштаба по оси времени внешний вид графика не изменяется, уменьшается только среднеквадратическое значение шума вследствие уменьшения ширины временного окна наблюдения.
В отличие от этого, график реализации коррелированного шума изменяет свой внешний вид в зависимости от ширины окна наблюдения (рис. 4.5, вверху). Коррелированный шум с заданной автокорреляционной функцией можно получить из белого, пропустив его через фильтр с заранее рассчитанной передаточной характеристикой.
Многократные измерения с усреднением всегда выполняются на конечном интервале времени 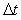 . Если случайная погрешность не коррелирована, то ее математическое ожидание равно нулю и не зависит от величины интервала . Если случайная погрешность не коррелирована, то ее математическое ожидание равно нулю и не зависит от величины интервала 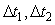 (рис. 4.5) и момента начала измерения. Поэтому усреднение по формуле (3.2) может дать неограниченное уменьшение случайной составляющей погрешности измерений с ростом числа измерений. (рис. 4.5) и момента начала измерения. Поэтому усреднение по формуле (3.2) может дать неограниченное уменьшение случайной составляющей погрешности измерений с ростом числа измерений.
Если же этот интервал усреднения 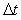 меньше времени корреляции (см. рис. 4.5, вверху), то на каждом отдельно взятом интервале усреднения меньше времени корреляции (см. рис. 4.5, вверху), то на каждом отдельно взятом интервале усреднения 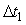 или или 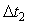 получим разные значения погрешности. В отличие от белого шума, погрешность среднего арифметического при увеличении количества измерений будет стремиться к некоторому значению получим разные значения погрешности. В отличие от белого шума, погрешность среднего арифметического при увеличении количества измерений будет стремиться к некоторому значению 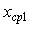 , , 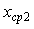 (рис. 4.5, вверху), отличному от нуля. Поэтому формула (3.2) перестает быть справедливой. (рис. 4.5, вверху), отличному от нуля. Поэтому формула (3.2) перестает быть справедливой.
Поскольку в реальных измерениях всегда присутствует, по крайней мере, фликкер-шум (что является фундаментальным законом природы [Букингем]), который делает шум измерений отличным от белого, то усреднение измерений не может снизить случайную составляющую погрешности до нуля. Кроме того, в цифровых средствах измерений всегда присутствует помеха с частотой тактового генератора, которая придает окраску белому шуму.
Предположим, что измерения выполняются в течение конечного промежутка времени  (т. е. во временном окне шириной (т. е. во временном окне шириной  ) и за это время выполняется ) и за это время выполняется 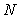 измерений с равными интервалами измерений с равными интервалами 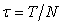 между ними, после чего находится среднее значение между ними, после чего находится среднее значение 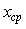 (4.39). Предположим для простоты, что измеряемая величина равна нулю, т.е. в результате измерений мы получаем только величину случайной погрешности, которую обозначим (4.39). Предположим для простоты, что измеряемая величина равна нулю, т.е. в результате измерений мы получаем только величину случайной погрешности, которую обозначим 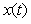 . .
Найдем среднеквадратическое отклонение погрешности 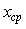 . Для этого выполним множество измерений сериями по . Для этого выполним множество измерений сериями по 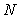 , выполняя усреднение в пределах каждой серии. В результате получим множество значений , выполняя усреднение в пределах каждой серии. В результате получим множество значений 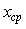 . .
Измерение будем выполнять в моменты времени 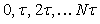 (рис. 4.6, слева). Обратим внимание, что измерение в моменты времени (рис. 4.6, слева). Обратим внимание, что измерение в моменты времени 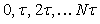 эквивалентно измерению в один и тот же момент времени эквивалентно измерению в один и тот же момент времени 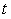 (рис. 4.6, справа), если использовать линии задержки, которые будут сдвигать реализацию случайного процесса на (рис. 4.6, справа), если использовать линии задержки, которые будут сдвигать реализацию случайного процесса на 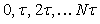 . Поэтому результат усреднения измерений, выполненных за время . Поэтому результат усреднения измерений, выполненных за время 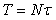 можно записать в виде можно записать в виде
 , , |
(4.46)
|
где 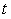 - момент времени выполнения измерений. - момент времени выполнения измерений.
Функцию 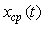 можно описать с помощью спектральной плотности мощности, для чего сначала найдем ее Фурье-изображение: можно описать с помощью спектральной плотности мощности, для чего сначала найдем ее Фурье-изображение:
где сначала использована замена переменной 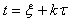 , затем введено обозначение , затем введено обозначение 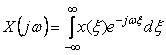 Фурье-изображения рассматриваемой случайной погрешности Фурье-изображения рассматриваемой случайной погрешности 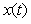 . .
Полученное выражение можно записать в виде
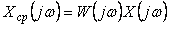 , , |
(4.48)
|
где
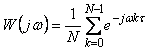 . . |
(4.49)
|
Таким образом, процесс усреднения можно рассматривать как прохождение случайного процесса через усредняющий фильтр с передаточной характеристикой (4.49). Поскольку вследствие симметрии Фурье изображений в (4.48) относительно оси ординат 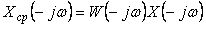 , то, умножая левую и правую часть этого выражения на соответствующие части в (4.48). получим: , то, умножая левую и правую часть этого выражения на соответствующие части в (4.48). получим:
 , , |
(4.50)
|
откуда
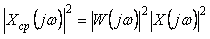 . . |
(4.51)
|
Пользуясь определением спектральной плотности мощности (4.15), из последнего выражения получим
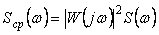 , , |
(4.52)
|
где 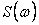 и и 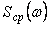 - спектральные плотности мощности случайной составляющей погрешности до процесса усреднения и после. - спектральные плотности мощности случайной составляющей погрешности до процесса усреднения и после.
Рассмотрим передаточную функцию усредняющего фильтра (4.49). Используя формулу суммы членов геометрической прогрессии 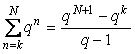 , ее можно записать в виде , ее можно записать в виде
Пользуясь соотношением 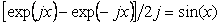 , окончательно получим , окончательно получим
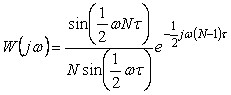 . . |
(4.54)
|
Выражение (4.54) является передаточной функцией цифрового sinc-фильтра [Сергиенко], т. е. усреднение измерений, полученных в 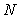 точках, отстоящих друг от друга на точках, отстоящих друг от друга на 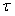 , эквивалентно цифровой фильтрации в прямоугольном окне шириной , эквивалентно цифровой фильтрации в прямоугольном окне шириной 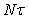 . В результате фильтрации ослабляются спектральные составляющие погрешности измерений, расположенные выше граничной частоты фильтра. . В результате фильтрации ослабляются спектральные составляющие погрешности измерений, расположенные выше граничной частоты фильтра.
Дисперсию погрешности измерений можно найти, интегрируя спектральную плотность мощности погрешности по всей полосе частот, от 0 до 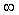 (см. (4.18)): (см. (4.18)):
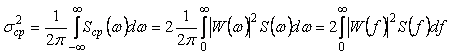 . . |
(4.55)
|
Это выражение справедливо для погрешности с любой спектральной плотностью. Предположим сначала, что погрешность является белым шумом, т.е. 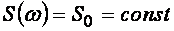 . Тогда, подставляя (4.54) в (4.55), получим . Тогда, подставляя (4.54) в (4.55), получим
откуда
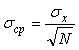 . . |
(4.57)
|
Это выражение совпадает с ранее полученным выражением (3.2), поскольку использовано предположение о преобладании белого шума. Таким образом, усреднение 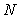 однократных измерений при белом шуме уменьшает погрешность в однократных измерений при белом шуме уменьшает погрешность в 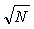 раз. раз.
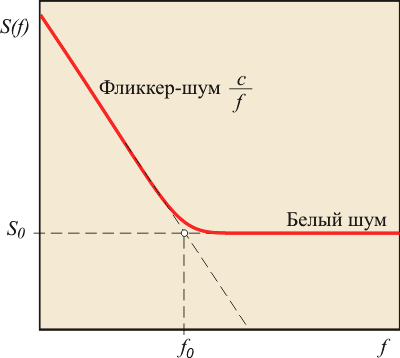
Предположим теперь, что случайная составляющая погрешности измерений обусловлена смесью белого шума со спектральной плотностью 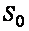 и фликкер-шума со спектральной плотностью и фликкер-шума со спектральной плотностью 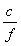 , где , где 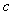 - константа, определяемая экспериментально (рис. 4.7). Тогда спектральную плотность мощности погрешности можно выразить как - константа, определяемая экспериментально (рис. 4.7). Тогда спектральную плотность мощности погрешности можно выразить как
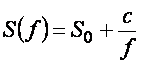 . . |
(4.58)
|
Найдем частоту 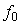 , на которой оба компонента шума одинаковы (рис. 4.7): , на которой оба компонента шума одинаковы (рис. 4.7):
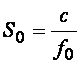 , откуда , откуда 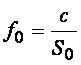 . . |
(4.59)
|
|
|
|
Рис. 4.7. Спектральная плотность мощности погрешности измерений в виде смеси белого и фликкер-шума
|
При 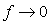 спектральная плотность мощности (4.58) стремится к бесконечности, поэтому интеграл (4.55) для фликкер-шума расходится. Однако, если учесть, что измерительные каналы систем автоматизации имеют режим автокалибровки, то низкочастотные компоненты фликкер-шума будут подавлены. Это позволяет выбрать ненулевую нижнюю границу спектра фликкер-шума, равную спектральная плотность мощности (4.58) стремится к бесконечности, поэтому интеграл (4.55) для фликкер-шума расходится. Однако, если учесть, что измерительные каналы систем автоматизации имеют режим автокалибровки, то низкочастотные компоненты фликкер-шума будут подавлены. Это позволяет выбрать ненулевую нижнюю границу спектра фликкер-шума, равную 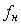 . Если калибровка в процессе эксплуатации прибора не выполняется, то величина . Если калибровка в процессе эксплуатации прибора не выполняется, то величина 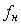 будет определяться межповерочным интервалом средства измерений. будет определяться межповерочным интервалом средства измерений.
Многократные измерения можно рассматривать как процесс дискретизации шума. Поскольку согласно теореме Котельникова для сохранения информации в дискретизированном сигнале частота отсчетов должна быть не менее удвоенной верхней частоты спектра сигнала, а шум имеет неограниченный спектр, то условие теоремы не выполняются и спектр шума после дискретизации будет сильно искажен вследствие алиасного эффекта. Однако, благодаря некоррелированности белого шума его отсчеты в любые моменты времени будут некоррелированы между собой, т.е. при дискретизации белого шума получается также белый шум. Наложение спектров вследствие алиасного эффекта также не придает окраску белому шуму, поскольку белый шум описывается функцией 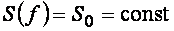 . .
Спектр фликкер-шума после дискретизации в общем случае будет сильно искажен и будет представлять собой сумму сдвинутых друг относительно друга спектров исходного шума (см. раздел "Алиасные частоты, антиалиасные фильтры" и формулу (4.97)). Однако, чтобы упростить анализ, воспользуемся тем, что в области частот 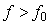 преобладает белый шум, а при преобладает белый шум, а при 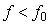 - фликкер-шум. Тогда можно считать, что спектр фликкер-шума ограничен частотой - фликкер-шум. Тогда можно считать, что спектр фликкер-шума ограничен частотой 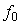 , а частота дискретизации всегда больше , а частота дискретизации всегда больше 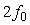 , т. е. условия теоремы Котельникова выполнены и спектр фликкер-шума не искажается. Дисперсию погрешности измерений в условиях преобладания фликкер-шума можно найти из соотношения (4.55): , т. е. условия теоремы Котельникова выполнены и спектр фликкер-шума не искажается. Дисперсию погрешности измерений в условиях преобладания фликкер-шума можно найти из соотношения (4.55):
где 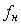 - нижняя граничная частота фликкер-шума; - нижняя граничная частота фликкер-шума; 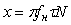 ; ; 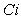 - интегральный косинус: - интегральный косинус: 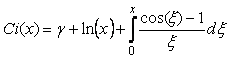 , где , где 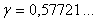 - постоянная Эйлера. - постоянная Эйлера.
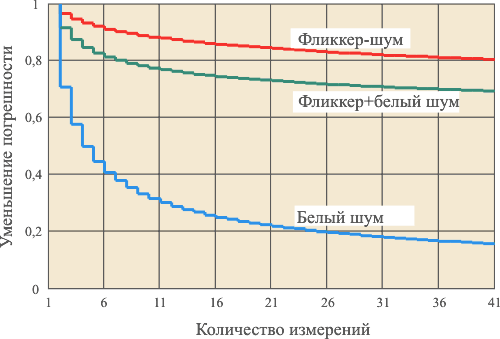
Нормируем значение 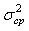 на на 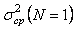 . Тогда графики зависимости коэффициента уменьшения погрешности . Тогда графики зависимости коэффициента уменьшения погрешности 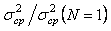 от количества измерений, построенные по формулам (4.60) и (3.2), будут иметь вид, приведенный на рис. 4.8. При построении графиков использованы следующие исходные данные: от количества измерений, построенные по формулам (4.60) и (3.2), будут иметь вид, приведенный на рис. 4.8. При построении графиков использованы следующие исходные данные: 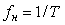 , где , где  =24 час., =24 час., 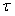 =1 с; параметр =1 с; параметр 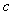 при нормировании сокращается. Напомним, что формула (4.60) получена в предположении, что частота измерений превышает величину при нормировании сокращается. Напомним, что формула (4.60) получена в предположении, что частота измерений превышает величину 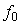 . Как видим, если при белом шуме усреднение 25 измерений дает снижение погрешности в 5 раз, то при наличии фликкер-шума - только в 1,2 раза. . Как видим, если при белом шуме усреднение 25 измерений дает снижение погрешности в 5 раз, то при наличии фликкер-шума - только в 1,2 раза.
При белом шуме эффективность усреднения не зависит от ширины усредняющего окна, а зависит только от количества отсчетов (4.57). При наличии фликкер-шума эффективность усреднения начинает зависеть от ширины временного окна 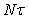 , причем увеличение его ширины менее эффективно, чем для белого шума, поскольку спектральная плотность мощности шума 1/f быстро возрастает с уменьшением частоты. Указанный эффект проявляется, в частности, в том, что различие среднего значения 100 результатов измерений, выполненных в течение 10 сек, будут сильно отличаться от среднего 100 измерений, выполненных за 10 суток. Погрешность, обусловленная фликкер-шумом, может быть существенно снижена только при условии, что ширина временного окна , причем увеличение его ширины менее эффективно, чем для белого шума, поскольку спектральная плотность мощности шума 1/f быстро возрастает с уменьшением частоты. Указанный эффект проявляется, в частности, в том, что различие среднего значения 100 результатов измерений, выполненных в течение 10 сек, будут сильно отличаться от среднего 100 измерений, выполненных за 10 суток. Погрешность, обусловленная фликкер-шумом, может быть существенно снижена только при условии, что ширина временного окна  превышает величину межкалибровочного интервала средства измерений. превышает величину межкалибровочного интервала средства измерений.
Из вышеизложенного можно сделать следующие выводы.
- Увеличение точности путем усреднения результатов многократных измерений ограничено не только систематической составляющей погрешности, но и спектральным составом шума измерений. Фликкер-шум, спектральная плотность мощности которого растет с понижением частоты, ограничивает возможность увеличения точности путем усреднения.
- Наиболее практичным способом устранения погрешности, обусловленной фликкер-шумом, является периодическая автокалибровка средства измерений.
- Погрешность усреднения в случае некоррелированной погрешности не зависит от ширины временного окна
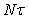 , а зависит только от количества отсчетов , а зависит только от количества отсчетов 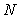 . .
- Усреднение может применяться только при постоянном значении измеряемой величины. В противном случае нужно учитывать динамическую погрешность (см. следующий параграф) или уменьшать ширину окна усреднения.
- Усреднение является разновидностью цифровой фильтрации методом "скользящего среднего", поэтому может быть использовано и при наличии шумов объекта измерений. Этой проблеме посвящена специальная литература [Сергиенко].
|
|

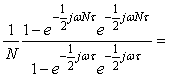
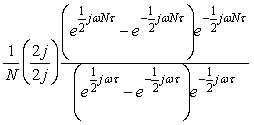
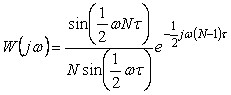 .
.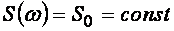 . Тогда, подставляя (4.54) в (4.55), получим
. Тогда, подставляя (4.54) в (4.55), получим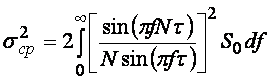
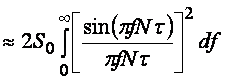 =
=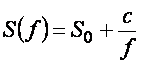 .
.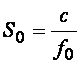 , откуда
, откуда 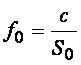 .
.
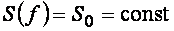 .
.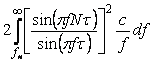 =
=