4.1. Основные понятия
4.1.1. Определения основных терминов
Метрология использует понятия, которые требуют точных и однозначных определений. С течением времени происходит уточнение понятий и их определения закрепляются в стандартах, рекомендациях по стандартизации и метрологических инструкциях. Основные термины и определения современной метрологии установлены в рекомендациях по метрологии РМГ 29-99 [РМГ], введенных в действие 1 января 2001 г. взамен ГОСТ 16263-70.
Измерение - это совокупность операций, обеспечивающих нахождение соотношения измеряемой величины с ее единицей измерения и получение значения этой величины. Измерение выполняется с помощью технического средства, хранящего единицу физической величины.
Контроль - это операции по определению соответствия характеристик изделия установленным нормам. Контроль включает в себя проведение измерений, испытаний или проверки характеристик изделия. Результатом контроля является заключение о соответствии или несоответствии. Может быть получено несколько градаций состояния соответствия. Контроль характеризуется достоверностью, т.е. степенью доверия к его результатам. Если контроль выполняется с помощью средств измерений, он называется измерительным контролем.
Индикатор - это техническое средство, предназначенное для установления наличия какой-либо физической величины или превышения уровня ее порогового значения. Например, индикатор может выдавать сигнал о превышении уровня загазованности котельной порогового значения.
Измерительная система - совокупность функционально объединенных мер, измерительных приборов, измерительных преобразователей, ЭВМ и других технических средств, размещенных в разных точках контролируемого объекта и т.п. с целью измерений одной или нескольких физических величин, свойственных этому объекту, и выработки измерительных сигналов в разных целях.
Примером измерительной системы может быть радионавигационная система для определения местоположения различных объектов, состоящая из ряда измерительно-вычислительных комплексов, разнесенных в пространстве на значительное расстояние друг от друга.
В зависимости от назначения измерительные системы разделяют на измерительные информационные, измерительные контролирующие, измерительные управляющие и др.
Измерительно-вычислительный комплекс (ИВК) - функционально объединенная совокупность средств измерений, ЭВМ и вспомогательных устройств, предназначенная для выполнения в составе измерительной системы конкретной измерительной задачи.
Измерительный канал - совокупность технических средств измерительной системы, которая выполняет законченную функцию от восприятия измеряемой величины до получения результата измерения, выраженного числом или соответствующим ему кодом.
Точность измерений - основная характеристика качества средств измерений, которая характеризует степень близости результата измерения к истинному значению измеряемой величины. Точность можно представить как величину, обратную модулю относительной погрешности, однако количественное выражение точности используется редко, обычно говорят "высокая точность, низкая точность", а для численного описания точности используют понятие погрешности.
Погрешность измерений - величина отклонения результата измерения от истинного значения измеряемой величины.
Предел допускаемой погрешности - границы зоны, за которую не должна выходить погрешность с вероятностью, равной единице. Параметр средства измерений.
Косвенные измерения - измерения, при которых результат определяется по известной зависимости между искомой величиной (т. е. величиной, которую надо найти) и измеряемыми величинами. Например, измерение сопротивления путем измерения напряжения и тока с последующим нахождением их отношения является косвенным измерением.
Совместные измерения - проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними. Например, измерение вольтамперной характеристики диода. Для определения параметров зависимости обычно используют метод наименьших квадратов.
Совокупные измерения - проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Пример: измерение сопротивления двух резисторов по результатам измерения измерений суммарного сопротивления их последовательного и параллельного соединения.
Инструментальная, или аппаратная погрешность - погрешность средства измерения. Делится на основную и дополнительную.
Основная погрешность измеряется и нормируется в нормальных условиях эксплуатации (при температуре 20 ºС, атмосферном давлении 760 мм. рт. ст., относительной влажности 60 % - по ГОСТ 8.395 [ГОСТ]).
Дополнительная погрешность учитывает влияние внешних факторов - температуры, давления, напряжения источника питания, влажности, утечки входных каскадов измерительного преобразователя и др.
Погрешность метода измерений (методическая погрешность) - Составляющая систематической погрешности измерений, обусловленная несовершенством принятого метода измерений. Погрешность метода иногда называют теоретической погрешностью.
Динамическая погрешность возникает, когда измеряемая величина не постоянна во времени. Для ее описания используют, например, импульсную или переходную характеристику средства измерения или их изображения по Лапласу и Фурье. Увеличивается при приближении частоты измеряемого сигнала к границе полосы пропускания измерительного канала.
Систематическая погрешность - погрешность, величина которой остается постоянной от измерения к измерению и которая может быть обнаружена с помощью поверки или калибровки и затем скомпенсирована. Примером является погрешность нелинейности термопары, которая компенсируются с помощью таблиц поправок в контроллере измерительного модуля.
Систематические погрешности обычно изменяются с течением времени (дрейфуют), что делает необходимым периодическую калибровку измерительных приборов. Эти изменения вызваны процессами старения и износа элементов измерительных устройств. Старение может привести к увеличению погрешности в 1,25...2,5 раза [Новицкий]. Систематические погрешности выявляются путем сравнения результатов измерений с аналогичными результатами, выполненными образцовым прибором или путем измерений с помощью других приборов, работающих на иных физических принципах.
Систематическая погрешность являются случайной величиной на множестве приборов одного типа и детерминированной для отдельного образца средства измерений. Поэтому в паспорте прибора она может быть указана в виде математического ожидания и среднеквадратического отклонения.
Случайные погрешности не могут быть предсказаны, т.е. являются случайными величинами. Они обнаруживаются в виде различия результатов отдельных измерений при многократных измерениях. Основной их причиной являются помехи внутри измерительного прибора и собственные шумы электронных компонентов. В эксплуатационной документации указывают среднеквадратическое отклонение случайной составляющей погрешности или, для более точного описания, нормализованную автокорреляционную функцию или функцию спектральной плотности. Некоррелированные случайные погрешности могут быть уменьшены путем усреднения результатов многократных измерений.
Промах - погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Иногда вместо термина "промах" применяют термин "грубая ошибка" измерений.
Абсолютная погрешность измерительного прибора определяется как разность между измеренным с его помощью и точным значением измеряемой величины. Абсолютная погрешность имеет размерность измеряемой величины.
Относительная погрешность выражается в процентах от текущего значения измеряемой величины.
Порог чувствительности - наименьшее значения физической величины, начиная с которого может осуществляться ее измерение данным средством.
Приведенная погрешность - это отношение абсолютной погрешности к верхнему пределу диапазона измерений для симметричных диапазонов измерений или к ширине диапазона для несимметричных.
Если абсолютная погрешность не изменяется при изменении измеряемой величины, то для ее учета она складывается с результатом измерений. Такая погрешность называется аддитивной. Примером аддитивной погрешности является погрешность, вызванная смещением нуля операционного усилителя.
Погрешность может увеличиваться с ростом значений измеряемой величины. Такую погрешность учитывают путем умножения результата измерений на величину погрешности и называют мультипликативной. Примером мультипликативной погрешности является погрешность коэффициента передачи измерительного преобразователя. Мультипликативная относительная погрешность является постоянной величиной. Мультипликативная и аддитивная погрешности обычно являются параметрами линейной зависимости, позволяющей рассчитать результирующую погрешность средства измерений. Итоговая абсолютная погрешность измерений находится по формуле
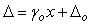 , , |
(4.1)
|
где 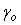 - мультипликативная погрешность, - мультипликативная погрешность, 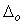 - аддитивная погрешность, - аддитивная погрешность, 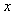 - значение измеряемой величины. - значение измеряемой величины.
Приведенную погрешность тоже можно представить состоящей из мультипликативной и аддитивной компоненты:
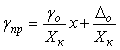 , , |
(4.2)
|
где 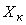 - верхний предел диапазона измерений для симметричных диапазонов измерений или ширина диапазона для несимметричных. - верхний предел диапазона измерений для симметричных диапазонов измерений или ширина диапазона для несимметричных.
Аналогично можно представить и относительную погрешность:
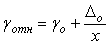 . . |
(4.3)
|
При малых значениях измеряемой величины погрешность измерений определяется абсолютной погрешностью, при больших - относительной.
В некоторых случаях зависимость погрешности от значения измеряемой величины является более сложной, чем это можно учесть с помощью формулы (4.1). Тогда используют более сложные зависимости. Например, для мегаомметра максимальная точность оказывается не у верхнего предела измерений, а посередине диапазона, поскольку с ростом значений измеряемой величины 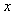 (сопротивления) растет входное сопротивление прибора, следовательно, с увеличением (сопротивления) растет входное сопротивление прибора, следовательно, с увеличением 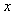 растет и погрешность измерений. В таких случаях формула для погрешности приобретает вид растет и погрешность измерений. В таких случаях формула для погрешности приобретает вид
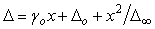 , , 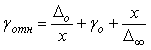 . . |
(4.4)
|
где 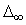 - верхний порог чувствительности. - верхний порог чувствительности.
Нормированное значение погрешности - это величина погрешности, которая учитывает технологический разброс серии изготавливаемых измерительных приборов и является предельной для всех приборов данного типа. Погрешность любого прибора из данной серии может быть меньше предельной, но не может превышать ее. Нормированное значение погрешности заносится в паспорт прибора.
Номинальная характеристика - распространяющаяся на все средства измерений данного типа, в отличие от индивидуальной характеристики, которая распространяется только на конкретный экземпляр прибора.
Класс точности указывает нормированное значение погрешности в процентах. Однако класс точности учитывает целую совокупность метрологических характеристик, таких как, например, нестабильность погрешности в течение года, сопротивление изоляции, и др. [ГОСТ]. Класс точности 0,1 может быть присвоен прибору, имеющему погрешность 0,1%. Для указания мультипликативной погрешности класс точности помещается в кружок, для указания аддитивной погрешности указывается просто число без дополнительных символов.
Вариация показаний измерительного прибора - разность показаний прибора в одной и той же точке диапазона измерений при плавном подходе к этой точке со стороны меньших и больших значений измеряемой величины.
Диапазон измерений - область значений измеряемой величины, в пределах которых нормированы допускаемые пределы погрешности средства измерений.
Динамический диапазон - это отношение предела измерения к порогу чувствительности, обычно выражается в децибелах. Для измерений в широком динамическом диапазоне используют измерительные приборы с переключаемыми диапазонами измерений. Во время переключения диапазонов происходит изменение схемы соединения элементов, при которой динамический диапазон сдвигается в сторону больших или меньших значений измеряемой величины. В автоматизированных системах переключение диапазонов измерений выполняется автоматически, по программе, записанной в компьютер или контроллер. В качестве примера см. руководство на модуль NL-8AI .
Воспроизводимость результатов измерений характеризует близость результатов измерений, выполненных различными средствами в разное время в разных местах. Оценка воспроизводимости позволяет выявить грубые ошибки в процессе измерений или некорректно поставленные методики измерений, влияние трудно учитываемых внешних факторов.
Калибровка - совокупность операций, позволяющих определить поправки к показаниям средства измерений или оценить погрешность этих средств.
Поверка - установление официально уполномоченным органом пригодности средства измерений к применению. Поверке подвергают средства измерений, подлежащие государственному метрологическому контролю и надзору.
4.1.2. Точность, разрешающая способность и порог чувствительности
При выборе модулей ввода-вывода аналоговых сигналов по критерию точности, разрешающей способности и чувствительности необходимо понимать различие этих терминов. Типовое заблуждение состоит в том, что "если модуль ввода имеет погрешность ±0,05%, то разрядность его АЦП более чем 12 бит плюс знак 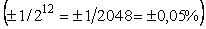 является бесполезной". Покажем, что это не так. является бесполезной". Покажем, что это не так.
Точность (погрешность) характеризует степень отличия результата измерения от точного значения, связанного с эталоном единицы физической величины. Разрешающая же способность показывает, какое минимальное отклонение измеряемой величины может быть зарегистрировано измерительным прибором. Например, если модуль ввода в диапазоне измерений -10...+10 В имеет погрешность ±0,05%, то его порог чувствительности равен ±5 мВ. Однако, благодаря наличию 16-разрядного АЦП этот модуль может различить два входных сигнала, отличающихся на 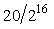 =0,3 мВ, т.е. его разрешающая способность в ±5/0,3=±16 раз выше порога чувствительности. Отметим, что это справедливо при условии, что уровень собственных шумов модуля ввода ниже величины младшего значащего разряда (МЗР), т.е. погрешность является чисто систематической. При большой случайной погрешности можно предпринять меры для ее уменьшения, например, с помощью усреднения результатов многократных измерений (см. раздел "Повышение точности путем усреднения результатов измерений"). =0,3 мВ, т.е. его разрешающая способность в ±5/0,3=±16 раз выше порога чувствительности. Отметим, что это справедливо при условии, что уровень собственных шумов модуля ввода ниже величины младшего значащего разряда (МЗР), т.е. погрешность является чисто систематической. При большой случайной погрешности можно предпринять меры для ее уменьшения, например, с помощью усреднения результатов многократных измерений (см. раздел "Повышение точности путем усреднения результатов измерений").
Порог чувствительности, который определяется погрешностью измерений, может быть гораздо больше, чем разрешающая способность, поскольку при определении погрешности учитывают:
- нелинейность измерительного прибора во всем диапазоне измерений;
- динамику процесса старения прибора;
- технологический разброс метрологических параметров от прибора к прибору;
- не только систематическую, но и случайную некоррелированную компоненту погрешности, которая может быть уменьшена до уровня МЗР путем многократных измерений с последующим усреднением результатов.
Разрешающая способность не зависит от перечисленных выше факторов и это объясняет ее отличие от порога чувствительности и погрешности.
Приведем несколько примеров, когда требования к погрешности на несколько порядков могут отличаться от требований к разрешающей способности.
Пример 1
Предположим, имеется релейный регулятор, который в соответствии с алгоритмом своей работы должен определить знак разности между температурой в печи и значением уставки. Если для измерения температуры используется термопара с датчиком температуры холодного спая, с погрешностью измерений 2 ºС, то для измерения температуры в диапазоне 0...100 ºС достаточно 50 уровней квантования, что может быть обеспечено 6-разрядным АЦП. Если же использовать 16-разрядный АЦП, то разрешающая способность по температуре составит 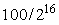 =0,0015 ºС. В случае применения 6-разрядного АЦП колебания температуры в процессе регулирования не могут быть менее 2 ºС, в то время как при использовании 16-разрядного АЦП амплитуда колебаний приближается к 0,0015 ºС. Такой регулятор используется, когда важна стабильность во времени, а не точность соответствия уставке. Например, стабильность (а не точность) важна для термостатов, которые используются при калибровке термодатчиков методом сличения с показаниями образцового прибора. Напомним, что альтернативным вариантом является калибровка с помощью калибратора (задатчика), который должен иметь высокую точность (и одновременно стабильность) задания температуры. =0,0015 ºС. В случае применения 6-разрядного АЦП колебания температуры в процессе регулирования не могут быть менее 2 ºС, в то время как при использовании 16-разрядного АЦП амплитуда колебаний приближается к 0,0015 ºС. Такой регулятор используется, когда важна стабильность во времени, а не точность соответствия уставке. Например, стабильность (а не точность) важна для термостатов, которые используются при калибровке термодатчиков методом сличения с показаниями образцового прибора. Напомним, что альтернативным вариантом является калибровка с помощью калибратора (задатчика), который должен иметь высокую точность (и одновременно стабильность) задания температуры.
Пример 2
В элеваторах для хранения растительного сырья наблюдается эффект самосогревания, связанный, в основном, с деятельностью микроорганизмов. Для обеспечения качества зерна абсолютное значение температуры достаточно знать с погрешностью в несколько градусов, но факт ее роста желательно фиксировать с разрешающей способностью 0,1...0,01 ºС. Высокая разрешающая способность позволяет предупредить развитие очага самосогревания на ранней стадии и расположить датчики температуры на большом расстоянии один от другого.
Пример 3
Если требуется обнаружить момент времени начала химической реакции по признаку начала роста температуры, то необходим прибор с высокой разрешающей способностью, но необязательно высокой точностью.
Пример 4
Пусть требуется оценить параметры колебательного процесса (декремент затухания колебаний, период колебаний, коэффициент нелинейных искажений, длительность переходного процесса, величину помехи на фоне полезного сигнала) - во всех перечисленных случаях находится соотношение ординат или абсцисс функции в разных ее точках, т. е. пропорции между отдельными частями графика, которые не зависят от самого значения функции. Поэтому такие измерения могут быть выполнены прибором, имеющим низкую точность, но высокую разрешающую способность. Дополнительным требованием в этом примере является достаточная линейность измерительного канала в рассматриваемом диапазоне.
Для улучшения разрешающей способности при низкой точности используется "электронная лупа" (аналогичный термин в фотоаппаратах называется "zoom"). В основе принципа работы электронной лупы лежит свойство любых нелинейностей 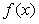 приближаться к линейным зависимостям приближаться к линейным зависимостям
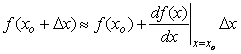 |
(4.5)
|
при малых 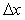 , что обеспечивает отсутствие нелинейных искажений формы исследуемого сигнала. Работа электронной лупы состоит в том, что из исследуемого сигнала вычитается некоторый постоянный уровень , что обеспечивает отсутствие нелинейных искажений формы исследуемого сигнала. Работа электронной лупы состоит в том, что из исследуемого сигнала вычитается некоторый постоянный уровень 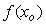 , а разность усиливается с помощью аналогового усилителя или квантуется АЦП с высокой разрядностью. При этом величина постоянного уровня может быть задана с низкой точностью, поскольку целью является измерение соотношений отдельных участков сигнала между собой, а не относительно единицы физической величины. , а разность усиливается с помощью аналогового усилителя или квантуется АЦП с высокой разрядностью. При этом величина постоянного уровня может быть задана с низкой точностью, поскольку целью является измерение соотношений отдельных участков сигнала между собой, а не относительно единицы физической величины.
Отметим, что понятие "разрешающая способность" отсутствует в РМГ 29-99 [РМГ]. Причина, вероятно, в том, что это понятие не связано с измерением как операцией сличения с эталоном, но связано с оценкой отношений между физическими величинами, ни одна из которых не является эталоном, что не относится к измерениям в смысле РМГ 29-9911.
Точность, разрешающая способность и порог чувствительности в общем случае выше у АЦП с большим числом двоичных разрядов, хотя прямой связи здесь нет. АЦП с высокой разрядностью может иметь большой уровень шумов, высокую нестабильность источника опорного напряжения и связанную с ними низкую точность.
4.1.3. Функция автокорреляции
Погрешности измерений, обусловленные наведенными помехами и собственными шумами электронных приборов, описываются с помощью математической теории, получившей название "теория случайных процессов". Напомним основные понятия этой теории, которые мы будем использовать в дальнейшем изложении и которые используются ГОСТ 8.009 [ГОСТ] при нормировании случайной составляющей погрешности измерений.
Отличительной чертой случайного процесса является невозможность предсказания его мгновенного значения. Поэтому отдельные реализации случайного процесса описываются случайными функциями 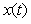 , значения которых в любой момент времени , значения которых в любой момент времени 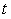 являются случайными величинами. Запись мгновенных значений случайного процесса на некоторый носитель информации (например, на жесткий диск компьютера) дает нам только одну реализацию случайного процесса, поскольку его повторные записи в тех же самых условиях показывают совсем другую функцию времени. Набор реализаций случайного процесса называется ансамблем. Невозможность аналитического описания случайных функций времени по причине чрезмерной их громоздкости делает необходимым применение статистического описания случайных процессов. являются случайными величинами. Запись мгновенных значений случайного процесса на некоторый носитель информации (например, на жесткий диск компьютера) дает нам только одну реализацию случайного процесса, поскольку его повторные записи в тех же самых условиях показывают совсем другую функцию времени. Набор реализаций случайного процесса называется ансамблем. Невозможность аналитического описания случайных функций времени по причине чрезмерной их громоздкости делает необходимым применение статистического описания случайных процессов.
Случайный процесс называется стационарным, если его статистические характеристики (математическое ожидание, среднеквадратическое отклонение и корреляционная функция) не изменяются с течением времени. Например, мгновенную погрешность средства измерений при постоянной температуре окружающей среды приближенно можно считать стационарным случайным процессом, поскольку среднеквадратическое отклонение и математическое ожидание погрешности не изменяются с течением времени, по крайней мере, в пределах межповерочного интервала.
В дальнейшем мы будем использовать только понятие стационарного эргодического случайного процесса, если иное специально не оговорено. Для эргодического процесса усреднение по ансамблю реализаций можно заменить усреднением по времени на интервале времени 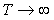 . Поэтому математическое ожидание эргодического случайного процесса определяется формулой . Поэтому математическое ожидание эргодического случайного процесса определяется формулой
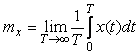 , , |
(4.6)
|
среднеквадратическое отклонение -
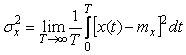 . . |
(4.7)
|
автокорреляционная функция -
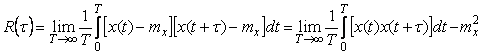 . . |
(4.8)
|
Коэффициент корреляции случайного процесса по определению равен
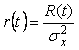 . . |
(4.9)
|
Как видно из определения, функция автокорреляции равна усредненному произведению реализации центрированного случайного процесса (т.е. процесса, из которого удалена постоянная составляющая 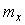 ) на свою копию, сдвинутую по времени на величину ) на свою копию, сдвинутую по времени на величину 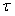 . Поэтому при . Поэтому при 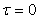 она равна дисперсии случайного процесса она равна дисперсии случайного процесса 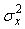 (сравните выражения (4.8) и (4.7)): (сравните выражения (4.8) и (4.7)):
 . . |
(4.10)
|
Если реализация случайного процесса 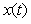 имеет ограниченный по частоте спектр, то при растяжении ее графика во времени наступает момент, когда он начинает выглядеть не как шум, а как извилистая гладкая кривая. Поэтому вероятность того, что при достаточно малом сдвиге имеет ограниченный по частоте спектр, то при растяжении ее графика во времени наступает момент, когда он начинает выглядеть не как шум, а как извилистая гладкая кривая. Поэтому вероятность того, что при достаточно малом сдвиге 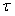 значения функции будут различаться сильно, становится пренебрежимо малой. При увеличении сдвига значения функции будут различаться сильно, становится пренебрежимо малой. При увеличении сдвига 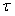 эта вероятность возрастает. Поэтому при малых эта вероятность возрастает. Поэтому при малых 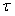 автокорреляционная функция всегда мало отличается от автокорреляционная функция всегда мало отличается от 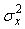 , а коэффициент корреляции - от единицы. , а коэффициент корреляции - от единицы.
Часто используется понятие "интервал корреляции" или "время корреляции", под которыми понимается величина временного сдвига 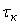 , при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента. Обычно интервал корреляции определяют как , при превышении которого корреляцией можно пренебречь в условиях конкретного эксперимента. Обычно интервал корреляции определяют как 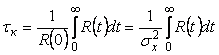 . .
 |
|
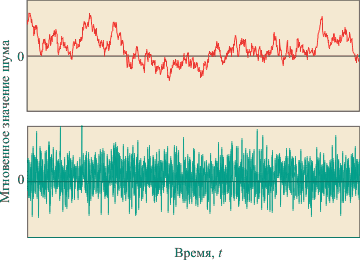
Рис. 4.1. Коррелированный (вверху) и некоррелированный (внизу) случайный процесс (погрешность измерений)
|
Если интервал корреляции равен нулю, то случайный процесс называют некоррелированным, или белым шумом. В противном случае случайный процесс является коррелированным. В качестве примера на рис. 4.1 приведен пример коррелированного (вверху) и некоррелированного (внизу) случайного процесса. Реальные процессы все являются коррелированными, поскольку имеют ограниченную мощность и, следовательно, ограниченную полосу частот. Однако на определенном интервале времени (частот) их можно приближенно считать некоррелированными.
Определения (4.6)-(4.9) используются только при теоретическом анализе случайных процессов, поскольку при реальных измерениях значения случайной величины всегда дискретны и количество измерений ограничено. Поэтому вместо математического ожидания, среднеквадратического отклонения и корреляционной функции используют соответствующие им выборочные значения, или оценки соответствующих статистических параметров, которые определяется по формулам:
оценка математического ожидания -
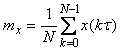 , , |
(4.11)
|
оценка среднеквадратического отклонения -
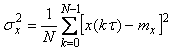 . . |
(4.12)
|
оценка автокорреляционной функции -
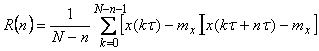 . . |
(4.13)
|
В пределе, при 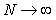 приведенные оценки параметров стремятся к их истинным значениям. В приведенных формулах для оценок параметров и самих параметров использованы одни и те же обозначения, поскольку в дальнейшем мы будем использовать только оценки, если иное не оговорено специально. приведенные оценки параметров стремятся к их истинным значениям. В приведенных формулах для оценок параметров и самих параметров использованы одни и те же обозначения, поскольку в дальнейшем мы будем использовать только оценки, если иное не оговорено специально.
Отдельно взятая реализация случайного процесса 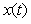 является детерминированной (неслучайной) функцией, поэтому для нее можно найти спектральную характеристику с помощью преобразования Фурье: является детерминированной (неслучайной) функцией, поэтому для нее можно найти спектральную характеристику с помощью преобразования Фурье:
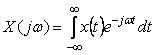 . . |
(4.14)
|
Однако функция 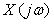 на практике не используется, поскольку она также сложна в описании, как и на практике не используется, поскольку она также сложна в описании, как и 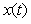 . Вместо нее используют понятие спектральной плотности мощности (энергетического спектра): . Вместо нее используют понятие спектральной плотности мощности (энергетического спектра):
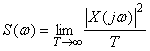 . . |
(4.15)
|
В соответствии с этим определением, спектральная плотность мощности шума измеряется в 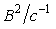 или или 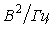 , , 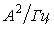 и т. п. Отметим, что в теории случайных процессов понятие мощности отличается от общепринятого: предполагается, что энергия шума выделяется на сопротивлении в 1 Ом, но размерность и т. п. Отметим, что в теории случайных процессов понятие мощности отличается от общепринятого: предполагается, что энергия шума выделяется на сопротивлении в 1 Ом, но размерность 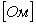 не указывается, поэтому вместо размерности мощности не указывается, поэтому вместо размерности мощности 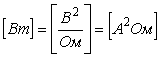 используется используется 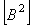 , , 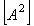 . Аналогично, энергия измеряется не в . Аналогично, энергия измеряется не в 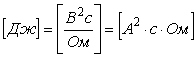 , а в , а в 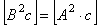 . .
Автокорреляционная функция 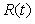 и спектральная плотность мощности и спектральная плотность мощности 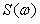 связаны между собой преобразованием Фурье (теорема Винера-Хинчина [Баскаков]): связаны между собой преобразованием Фурье (теорема Винера-Хинчина [Баскаков]):
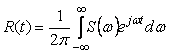 ; ; |
(4.16)
|
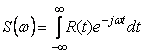 , , |
(4.17)
|
т. е. спектральная плотность мощности является Фурье-изображением корреляционной функции.
Поскольку 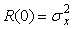 (см. (4.10)), подставив (см. (4.10)), подставив 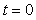 в формулу (4.16), получим в формулу (4.16), получим
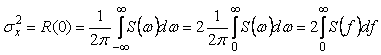 . . |
(4.18)
|
Здесь коэффициент 2 используется, когда нижний предел интегрирования заменяется на 0. Это возможно благодаря тому, что спектральная плотность мощности любого реального случайного процесса описывается четной функцией частоты [Букингем].
Если энергетический спектр лежит в диапазоне частот от 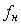 >0 до >0 до 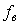 , например, благодаря применению фильтра, то можно считать, что за пределами указанного диапазона частот его значения равны нулю и это позволяет изменить пределы интегрирования в (4.16): , например, благодаря применению фильтра, то можно считать, что за пределами указанного диапазона частот его значения равны нулю и это позволяет изменить пределы интегрирования в (4.16):
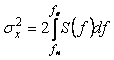 . . |
(4.19)
|
При использовании формул (4.16) и (4.19) надо помнить, что в ней применен двусторонний энергетический спектр (симметричный относительно начала оси ординат). В случае одностороннего спектра 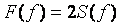 , заданного в диапазоне частот , заданного в диапазоне частот 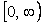 , коэффициент "2" должен отсутствовать: , коэффициент "2" должен отсутствовать:
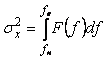 . . |
(4.20)
|
Это выражение позволяет найти среднеквадратическую погрешность измерения (например, напряжения 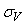 [Вольт]) в диапазоне частот [Вольт]) в диапазоне частот 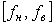 как как
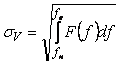 . . |
(4.21)
|
В зарубежной справочной литературе на графиках спектральной плотности мощности шума транзисторов, операционных усилителей и др. обычно по оси ординат откладывается корень квадратный из спектральной плотности мощности шума 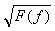 , имеющий размерность , имеющий размерность 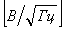 , , 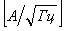 и т. п. В этом случае напряжение шума и т. п. В этом случае напряжение шума 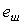 (среднеквадратическое значение) можно найти как (среднеквадратическое значение) можно найти как
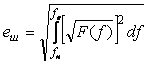 . . |
(4.22)
|
Для белого шума 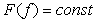 и предыдущее выражение упрощается: и предыдущее выражение упрощается:
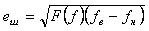 . . |
(4.23)
|
Эффективной шириной энергетического спектр называется величина 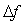 , определяемая по формуле , определяемая по формуле
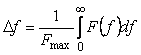 , , |
(4.24)
|
где 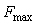 - максимальное значение функции - максимальное значение функции 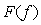 . Таким образом, эффективной шириной энергетического спектра . Таким образом, эффективной шириной энергетического спектра 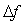 называют диапазон частот, в котором заключена такая же энергия, как и в диапазоне называют диапазон частот, в котором заключена такая же энергия, как и в диапазоне 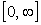 при условии, что в диапазоне при условии, что в диапазоне 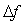 энергия имеет величину энергия имеет величину 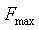 и распределена равномерно. и распределена равномерно.
В дальнейшем понятие случайного процесса будет использоваться для описания случайной погрешности измерений.
4.1.4. Коэффициент корреляции
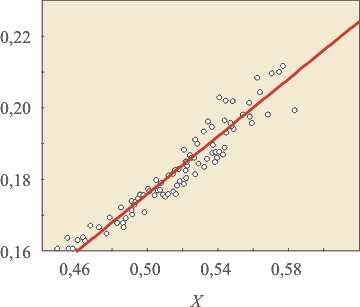
При расчете погрешности измерительного канала возникает задача суммирования погрешностей средств измерений, которые являются случайными величинами. Способ суммирования будет различным в зависимости от того, являются ли случайные величины статистически зависимыми. Понятие статистической зависимости иллюстрируется рис. 4.2: если с ростом одной случайной величины Х в среднем увеличивается (или уменьшается) и вторая (Y), то между этими величинами имеется статистическая зависимость. Для ее количественного описания используется понятие ковариации или коэффициента корреляции.
Рассмотрим суммирование двух случайных погрешностей 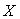 и и 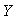 с нулевым математическим ожиданием (т. е. центрированных случайных величин). Дисперсия суммы двух случайных величин по определению равна математическому ожиданию квадрата их суммы: с нулевым математическим ожиданием (т. е. центрированных случайных величин). Дисперсия суммы двух случайных величин по определению равна математическому ожиданию квадрата их суммы:
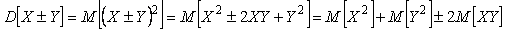 = = 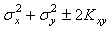 , , |
(4.25)
|
где 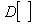 и и 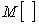 - операторы дисперсии и математического ожидания; - операторы дисперсии и математического ожидания; 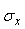 , , 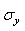 - среднеквадратические отклонения случайных величин - среднеквадратические отклонения случайных величин 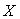 и и 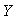 . Величина . Величина
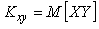 |
(4.26)
|
называется ковариацией ("совместной вариацией") случайных величин 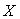 и и 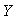 . .
Ковариацию дискретных случайных величин можно оценить по их дискретным значениям 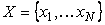 и и 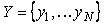 с помощью формулы среднего арифметического: с помощью формулы среднего арифметического:
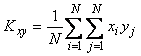 . . |
(4.27)
|
Коэффициентом корреляции 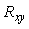 называют отношение ковариации к произведению среднеквадратических отклонений называют отношение ковариации к произведению среднеквадратических отклонений 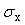 и и 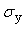 случайных величин случайных величин 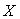 и и 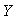 : :
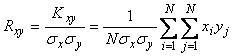 . . |
(4.28)
|
Когда случайные величины независимы, их коэффициент корреляции равен нулю, 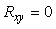 [Гмурман] и такие величины называются некоррелированными. Если коэффициент корреляции равен единице [Гмурман] и такие величины называются некоррелированными. Если коэффициент корреляции равен единице 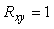 , то между величинами , то между величинами 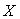 и и 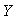 имеется не статистическая, а функциональная зависимость. имеется не статистическая, а функциональная зависимость.
Используя понятие среднеквадратического отклонения 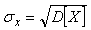 , уравнение (4.25) можно записать в виде , уравнение (4.25) можно записать в виде
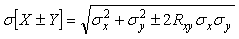 . . |
(4.29)
|
Здесь знак "-" используется когда случайные величины вычитаются, например, если находится разность напряжений двух измерительных каналов. При этом наличие корреляции между каналами частично уменьшает погрешность разности.
В случае, когда случайные величины статистически независимы (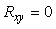 ), предыдущее выражение упрощается: ), предыдущее выражение упрощается:
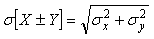 . . |
(4.30)
|
Такое суммирование называют геометрическим, поскольку оно выполняется аналогично нахождению гипотенузы прямоугольного треугольника.
Если коэффициент корреляции 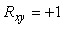 , то , то
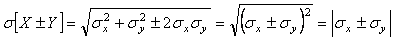 . . |
(4.31)
|
Если коэффициент корреляции равен 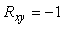 , то , то
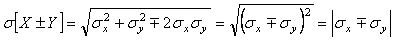 , , |
(4.32)
|
т.е. при нахождении суммы случайных величин отрицательный коэффициент корреляции уменьшает итоговую погрешность, а при нахождении разности - увеличивает.
Если случайные величины не центрированы и имеют математические ожидания 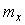 и и  , то коэффициент корреляции можно оценить как , то коэффициент корреляции можно оценить как
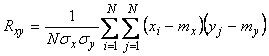 . . |
(4.33)
|
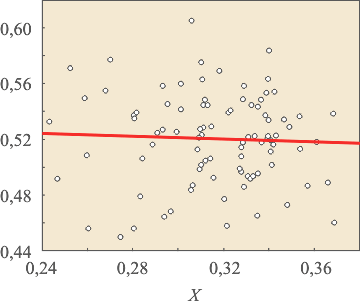
На рис. 4.2 показаны примеры статистической зависимости между случайными величинами при сильной (а) и слабой (б) корреляции. Точки на графике (значения случайной величины) могут группироваться очень близко к прямой линии, которая аппроксимирует эту зависимость, и тогда статистическая зависимость приближается к детерминированной. Степень отличия статистической зависимости от детерминированной характеризуют коэффициентом корреляции 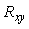 . .
|
|
|
|
(а)
|
(б)
|
|
Рис. 4.2. Примеры сильной (а), 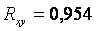 и слабой (б), и слабой (б), 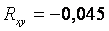 корреляции случайных величин корреляции случайных величин 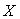 и и 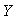 . Показана также прямая линия среднеквадратической регрессии . Показана также прямая линия среднеквадратической регрессии
|
Прямая линия, проведенная таким образом, что сумма квадратов отклонений значений случайной величины от этой линии минимальна, называется линией среднеквадратической регрессии. Тангенс угла наклона линии называется коэффициентом регрессии. Уравнение линии регрессии можно получить методом наименьших квадратов; оно имеет вид [Кремер]
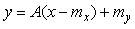 , ,
где 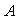 - коэффициент регрессии. Коэффициент регрессии вычисляется через коэффициент корреляции - коэффициент регрессии. Коэффициент регрессии вычисляется через коэффициент корреляции 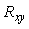 и среднеквадратические отклонения и среднеквадратические отклонения 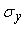 и и 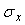 как как
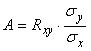 . . |
(4.34)
|
Коэффициент корреляции приобретает ясный физический смысл, если статистические переменные центрировать (вычесть математическое ожидание) и нормировать на величину среднеквадратического отклонения. Поскольку среднеквадратические отклонения нормированных величин равны единице, то коэффициент корреляции (4.33) становится равен тангенсу наклона линии среднеквадратической регрессии.
Статистическая зависимость между погрешностями средств измерений в общем случае нелинейная, однако этой нелинейностью обычно пренебрегают.
4.1.5. Точечные и интервальные оценки погрешности
|
|
|
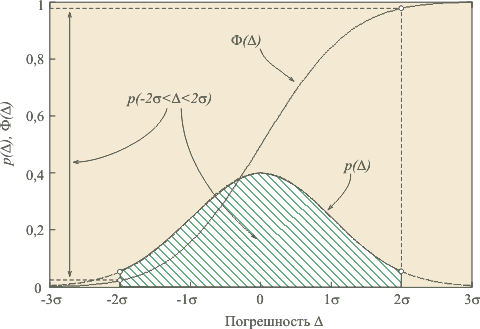
Рис. 4.3. Иллюстрация понятий доверительного интервала и доверительной вероятности
|
Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкам относится математическое ожидание погрешности и среднеквадратическое отклонение. В качестве интервальной оценки используют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью 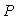 . Эта вероятность называется доверительной или надежностью оценки погрешности. . Эта вероятность называется доверительной или надежностью оценки погрешности.
Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.
Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.
Смысл интервальной оценки погрешности иллюстрируется рис. 4.3. Здесь использованы следующие обозначения:  - погрешность измерения; - погрешность измерения; 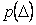 - плотность распределения погрешностей - плотность распределения погрешностей  ; ; 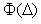 - функция распределения погрешностей, - функция распределения погрешностей,  . Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины . Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины  описывается функцией описывается функцией 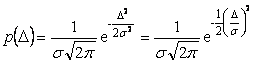 , где , где 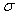 - среднеквадратическая погрешность. - среднеквадратическая погрешность.
Если погрешность измерения  находится внутри интервала находится внутри интервала 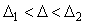 , то вероятность этого события вычисляется как , то вероятность этого события вычисляется как
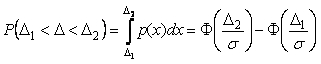 . . |
(4.35)
|
В наиболее типичном случае симметричных границ (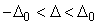 ) получим ) получим
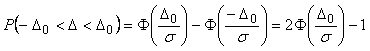 . . |
(4.36)
|
Здесь использовано свойство симметрии функции распределения для закона Гаусса.
Таким образом, если задан интервал 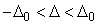 , который содержит в себе погрешность измеряемого параметра , который содержит в себе погрешность измеряемого параметра  , то вероятность того, что погрешность , то вероятность того, что погрешность  не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность 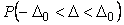 называют также надежностью оценки погрешности и обозначают символом называют также надежностью оценки погрешности и обозначают символом 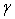 : :
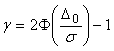 . . |
(4.37)
|
Для вычисления функции распределения удобно использовать пакеты MathCAD, Matlab. С их помощью из формулы (4.37) несложно найти величину доверительного интервала 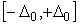 , если задана величина надежности , если задана величина надежности 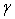 . .
Для 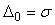 доверительная вероятность доверительная вероятность 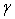 =68,3%; для =68,3%; для 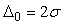 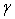 =95,3%; для =95,3%; для 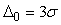 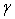 =99,7% и для =99,7% и для 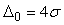 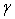 = 99,994%. = 99,994%.
Для увеличения надежности оценки погрешности измерений или для сужения доверительного интервала при заданной надежности можно использовать усреднение результатов многократных измерений. Поскольку оценка среднеквадратической погрешности результата усреднения 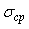 равна равна 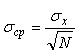 (см. (3.2)), где (см. (3.2)), где 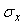 - среднеквадратическая погрешность средства измерений, - среднеквадратическая погрешность средства измерений, 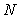 - количество однократных измерений, то, подставив в (4.37) вместо - количество однократных измерений, то, подставив в (4.37) вместо 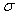 величину величину 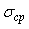 , получим , получим
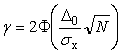 . . |
(4.38)
|
Эта формула позволяет найти количество однократных измерений 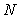 , которое необходимо усреднить для получения требуемого доверительного интервала , которое необходимо усреднить для получения требуемого доверительного интервала 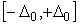 при заданной надежности при заданной надежности 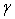 или требуемой надежности или требуемой надежности 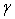 при заданном доверительном интервале при заданном доверительном интервале 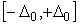 . Поскольку формула (4.38) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений. . Поскольку формула (4.38) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.
Следует иметь в виду, что повышение точности путем усреднения результатов многократных измерений имеет множество ограничений (см. п. "Многократные измерения").
Проблемой использования интервального метода оценки погрешности является необходимость знания закона распределения погрешностей.
Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений. Интересные примеры из истории определения расстояния до Солнца, заряда электрона и др. приводятся в книге [Тутубалин]. Ученые, которые делали эти выдающиеся измерения, указывали доверительные вероятности для оценки точности своих измерений. Однако ни одна из этих оценок не выдержала испытания временем: каждое новое, более точное измерение не укладывается в предсказанный ранее доверительный интервал. Это связано с тем, что систематическую погрешность или наличие ошибки в постановке эксперимента, в учете факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.
4.1.6. Погрешность метода измерений
Для выполнения автоматизированных измерений используют датчики и измерительные преобразователи, измерительные модули ввода аналоговых сигналов, обработку результатов измерений на компьютере или в контроллере. При этом на погрешность результата измерений оказывают влияние следующие факторы:
- сопротивление кабелей;
- соотношение между входным импедансом средства измерений и выходным импедансом датчика;
- качество экранирования и заземления, мощность источников помех;
- погрешность метода косвенных, совместных или совокупных измерений;
- наличие внешних влияющих факторов, если они не учтены в дополнительной погрешности средства измерений;
- погрешность обработки результатов измерений программным обеспечением.
Все погрешности, которые не могут быть учтены в процессе сертификационных испытаний и внесены в паспорт средства измерений, а появляются в конкретных условиях применения, относятся к методическим. В отличие от них, инструментальные погрешности нормируются в процессе производства измерительного прибора и заносятся в его эксплуатационную документацию. Таким образом, если в состав смонтированной автоматизированной измерительной системы входят средства измерений с нормированными погрешностями, то погрешность, вызванная перечисленными выше факторами, является методической. Если же выполняется сертификация всей измерительной системы, то методические погрешности могут быть учтены в погрешности всей системы и тогда они переходят в разряд инструментальных.
Для расчета или измерения методической погрешности трудно дать общие рекомендации. Каждый конкретный случай требует отдельного рассмотрения.
4.1.7. Погрешность программного обеспечения
Погрешность программного обеспечения (ПО) [МИ, МИ] оценивается как разность между результатами измерений, полученных данным ПО и эталонным ПО. Под эталонным понимается программное обеспечение, высокая точность которого доказана многократными испытаниями и тестированием. Понятие эталонного ПО является условным и определяется соглашением между заказчиком аттестации и исполнителем. В качестве эталонного может быть использовано ранее аттестованное ПО.
К основным источниками погрешностей ПО относятся:
- ошибки записи исходного текста программы и ошибки трансляции программы в объектный код;
- ошибки в алгоритме решения измерительной задачи;
- ошибки в таблицах для линеаризации нелинейных характеристик преобразования;
- применение неустойчивых или медленно сходящихся алгоритмов при решении плохо обусловленных измерительных задач;
- ошибки преобразования форматов данных;
- ошибки округления и др.
Надежность (достоверность) ПО обеспечивается средствами защиты от несанкционированных изменений, которые могут явиться причиной появления не учтенных при аттестации погрешностей.
4.1.8. Достоверность измерений
В процессе выполнения измерений могут появиться грубые ошибки (промахи), которые делают измерения недостоверными несмотря на применение очень точных измерительных приборов. Здесь под достоверностью понимается степень доверия к полученным результатам. Достоверность может быть низкая при наличии погрешностей, о существовании которых экспериментатор не догадывается. Достоверность при использовании автоматизированных измерительных систем снижается с ростом их сложности и существенно зависит от квалификации персонала проектирующей и монтажной организации.
Главным методом обеспечения достоверности является сопоставление результатов измерения одной и той же величины разными, не связанными друг с другом способами. Например, после монтажа системы измерения температуры в силосе элеваторе следует сравнить показания автоматизированной системы и автономного контрольного термометра, чтобы убедиться в правильности показаний автоматизированной системы.
Приведем несколько примеров, иллюстрирующих случаи, когда, несмотря на применение точных средств измерений, получаются совершенно ошибочные данные, вводящие человека в заблуждение.
Пример 1. Для измерения температуры воздуха в теплице использован датчик температуры с погрешностью ±0,5 ºС. Однако датчик установлен таким образом, что в некоторые часы на него падают прямые лучи солнца, которые нагревают датчик, но не изменяют температуру воздуха. При этом погрешность измерения температуры воздуха может составить +5 ºС, что позволяет квалифицировать результат измерения как недостоверный.
Пример 2. Для измерения температуры в силосах элеватора установлены точные датчики и сделан тщательный монтаж, но расположенный на крыше элеватора ретранслятор сотовой связи оказался незамеченным и не было принято достаточных мер для защиты от помех. При этом погрешность измерения температуры может составить ±10 ºС вследствие помех, наведенных передатчиком на сигнальных кабелях системы.
Пример 3. В автоматизированной системе для измерения параметров продукции использован модуль ввода с погрешностью ±0,05%, однако при наладке системы программист по ошибке установил частоту помехоподавляющего режекторного фильтра не 50, а 60 Гц. Объем проведенных приемо-сдаточных испытаний системы не позволил выявить эту ошибку. В результате погрешность измерений вследствие наведенной помехи с частотой 50 Гц может повыситься до ±10% вместо ожидаемых ±0,05%.
Пример 4. Во время выполнения измерений ваш коллега разговаривал по сотовому телефону. Наводка сигнала от передатчика сотового телефона может повысить погрешность измерений в несколько раз.
Пример 5. При монтаже системы заземлили экран сигнального кабеля с двух сторон. Объем проведенных приемо-сдаточных испытаний не позволил выявить эту ошибку. Погрешность может увеличиться в несколько раз по сравнению с ожидаемой.
Пример 6. В процессе эксплуатации системы нарушился контакт в цепи заземления, что привело к эпизодическому повышению уровня помех в измерительной цепи. В статье [Burleson] приводится пример, когда плохо затянутый болт в цепи заземления приводил к сбоям системы автоматики, причину которого искали несколько лет.
Пример 7. При расчете погрешности средств измерений была проигнорирована динамическая погрешность, поскольку исходные данные для ее расчета не были указаны в эксплуатационной документации на средство измерения и не были выявлены в процесс приемосдаточных испытаний ввиду сложности постановки эксперимента, отсутствия времени и приборов для контроля величины погрешности. Во время эксплуатации системы фактическая погрешность в несколько раз превышает расчетную.
В приведенных примерах сложно обнаружить наличие погрешности в процессе сдачи системы в эксплуатацию или она появляется в процессе эксплуатации. Это приводит к снижению достоверности измерений несмотря на высокую инструментальную точность использованных технических средств.
Общий подход к решению проблемы заключается в применении второй, независимой системы или методики измерений для обнаружения ошибок. Можно использовать также целый комплекс мер, включая подбор персонала, соблюдение графика поверки, тщательность выполнения типовых и сертификационных испытаний системы, соблюдение методики измерений и обслуживания измерительной системы.
Термин "достоверность" иногда используется во втором его значении - для указания вероятности того, что измеренное значение находится в заданном доверительном интервале [Новицкий] при условии, что все промахи и ошибки измерительной системы и методики измерений исключены. Количественным выражением достоверности в данном случае является доверительная вероятность. Следует различать эти два значения одного и того же термина.
|

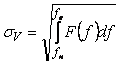 .
.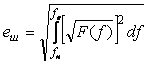 .
.


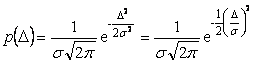 , где
, где 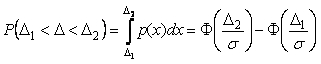 .
.






